D Dx 1 X 2 1 2
Juapaving
May 11, 2025 · 5 min read
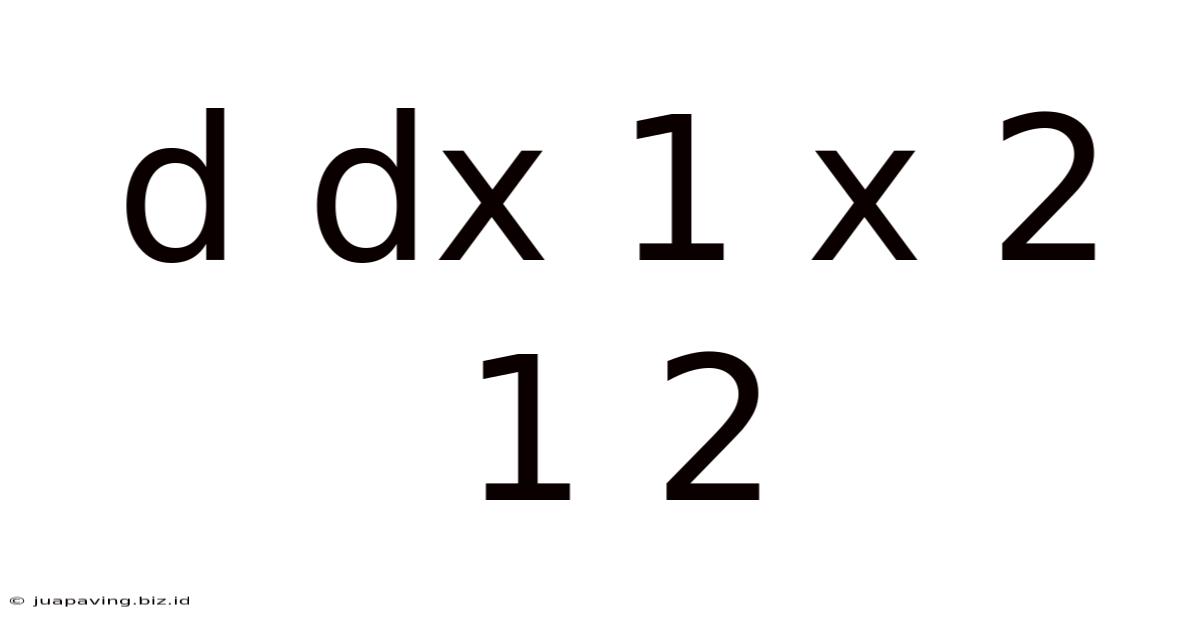
Table of Contents
Decomposing the Derivative: A Deep Dive into d/dx (1/(x² + 1))
The seemingly simple expression, d/dx (1/(x² + 1)), masks a rich tapestry of calculus concepts. This article will dissect this derivative, exploring various approaches, highlighting underlying principles, and demonstrating its applications. We'll journey from the fundamental rules of differentiation to more advanced techniques, offering a comprehensive understanding for both beginners and those seeking a deeper appreciation of differential calculus.
Understanding the Problem: d/dx (1/(x² + 1))
The notation d/dx signifies differentiation with respect to 'x'. We are tasked with finding the instantaneous rate of change of the function f(x) = 1/(x² + 1). This function, a rational function, represents a curve with specific properties that will become clearer as we proceed.
Method 1: The Quotient Rule
The most straightforward approach involves applying the quotient rule. This rule dictates how to differentiate a function that is a ratio of two other functions. The quotient rule states:
d/dx [u(x)/v(x)] = [v(x)u'(x) - u(x)v'(x)] / [v(x)]²
In our case, u(x) = 1 and v(x) = x² + 1. Therefore:
- u'(x) = d/dx (1) = 0
- v'(x) = d/dx (x² + 1) = 2x
Substituting these values into the quotient rule formula, we get:
d/dx (1/(x² + 1)) = [(x² + 1)(0) - (1)(2x)] / (x² + 1)² = -2x / (x² + 1)²
This is our final derivative using the quotient rule. It's a concise and accurate representation of the instantaneous rate of change of the original function.
Method 2: The Chain Rule and Negative Exponents
An alternative approach leverages the chain rule and the power rule of differentiation. First, rewrite the function using a negative exponent:
f(x) = (x² + 1)⁻¹
Now, apply the chain rule, which states:
d/dx [f(g(x))] = f'(g(x)) * g'(x)
Here, f(u) = u⁻¹ and g(x) = x² + 1. Therefore:
- f'(u) = -u⁻² = -1/u²
- g'(x) = 2x
Applying the chain rule:
d/dx [(x² + 1)⁻¹] = [-1/(x² + 1)²] * (2x) = -2x / (x² + 1)²
Again, we arrive at the same derivative, demonstrating the versatility of calculus techniques. This method highlights the power of algebraic manipulation in simplifying differentiation problems.
Exploring the Derivative: -2x / (x² + 1)²
The derivative, -2x / (x² + 1)², provides valuable insights into the behavior of the original function.
-
Critical Points: Setting the derivative equal to zero helps identify critical points (local maxima or minima). In this case, -2x / (x² + 1)² = 0 only when x = 0. This indicates a potential extremum at x = 0.
-
Increasing/Decreasing Intervals: Analyzing the sign of the derivative reveals where the original function is increasing or decreasing. For x > 0, the derivative is negative, indicating that the function is decreasing. For x < 0, the derivative is positive, implying the function is increasing.
-
Concavity: The second derivative provides information about the concavity of the function. We can differentiate -2x / (x² + 1)² using the quotient rule (again!) to find the second derivative. This is a more complex calculation, but the result will reveal the inflection points and the regions of concavity (concave up or concave down).
Applications of the Derivative
The derivative d/dx (1/(x² + 1)) = -2x / (x² + 1)² finds applications in numerous fields:
-
Physics: This derivative could represent the velocity of a particle whose position is described by the function 1/(x² + 1). Analyzing the derivative would allow us to understand the particle's motion, including its direction and speed.
-
Economics: In economic models, such functions might represent cost functions, demand curves, or other economic relationships. The derivative would give insights into marginal cost, marginal revenue, or the rate of change in demand.
-
Probability and Statistics: Functions similar to 1/(x² + 1) appear in probability distributions, specifically in the context of the Cauchy distribution. The derivative plays a crucial role in analyzing the properties and characteristics of this distribution.
Advanced Considerations: Taylor Series Expansion
The function 1/(x² + 1) can be represented using a Taylor series expansion around x = 0. This series provides a polynomial approximation of the function, which can be beneficial for various computations. The derivative plays a critical role in determining the coefficients of the Taylor series. The general formula for a Taylor series expansion is:
f(x) = Σ [f⁽ⁿ⁾(a)/n!] * (x - a)ⁿ
where:
- f⁽ⁿ⁾(a) represents the nth derivative evaluated at point 'a'.
- n! denotes the factorial of n.
- The summation runs from n = 0 to infinity.
Expanding 1/(x² + 1) around x = 0 using its derivatives (including the one we've calculated) would yield an infinite series representation of the function. This representation can be invaluable in solving complex mathematical problems or simulating the function's behavior within certain boundaries.
Conclusion: Beyond the Derivative
Our journey through the derivative of 1/(x² + 1) reveals much more than a simple calculation. It underscores the fundamental principles of calculus, the power of different differentiation techniques, and the valuable information extracted from derivatives. Understanding the function's behavior, its critical points, and its applications demonstrates the true significance of this seemingly straightforward mathematical operation. This exploration goes beyond a mere answer; it illuminates the deeper connections and far-reaching implications within the world of calculus. Furthermore, the techniques employed here, such as the quotient rule and chain rule, are fundamental to tackling a vast range of more complex derivative problems, equipping you with crucial skills for further mathematical exploration. Finally, the introduction of Taylor series expansion offers a glimpse into the sophisticated world of approximation and numerical analysis, showcasing the rich mathematical landscape surrounding this seemingly simple derivative.
Latest Posts
Latest Posts
-
Potato Is A Root Or Stem
May 12, 2025
-
How Many Degrees In Half A Circle
May 12, 2025
-
What Is It Called When A Solid Turns To Gas
May 12, 2025
-
What Are The Units Of Friction
May 12, 2025
-
What Is The Primary Electron Acceptor In Photosynthesis
May 12, 2025
Related Post
Thank you for visiting our website which covers about D Dx 1 X 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.