Conjugate Of A Complex Number In Polar Form
Juapaving
May 09, 2025 · 5 min read
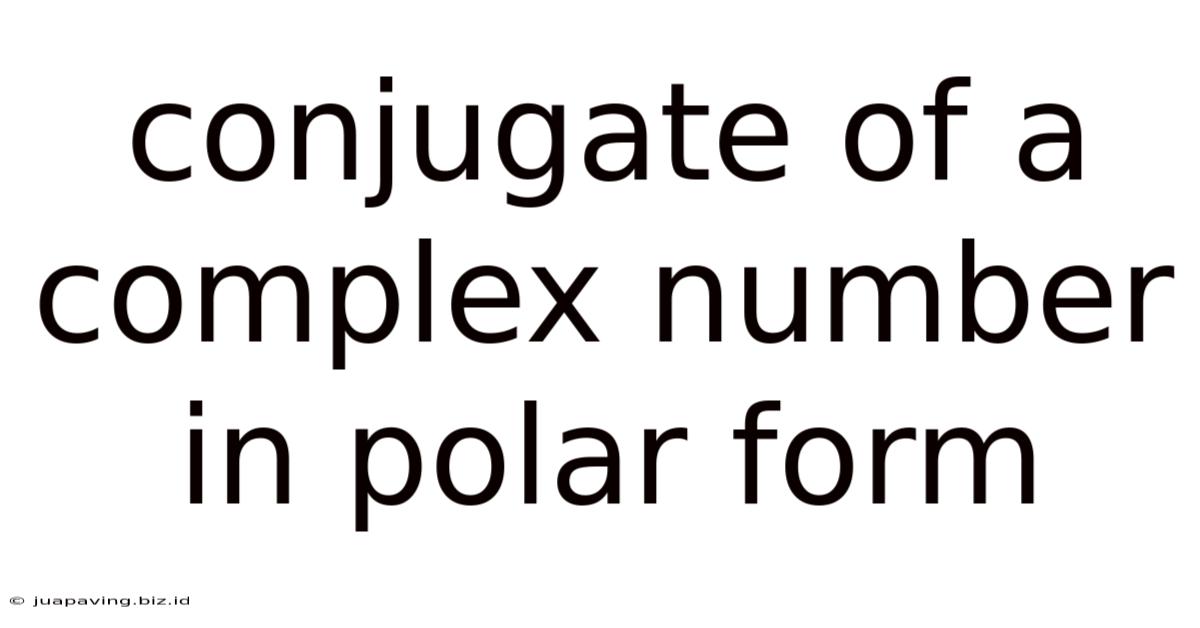
Table of Contents
Conjugate of a Complex Number in Polar Form: A Comprehensive Guide
The conjugate of a complex number is a fundamental concept in complex analysis with far-reaching applications in various fields, including electrical engineering, quantum mechanics, and signal processing. Understanding its properties, especially when expressed in polar form, is crucial for mastering advanced mathematical concepts. This comprehensive guide delves into the intricacies of the conjugate of a complex number in polar form, providing a detailed explanation with illustrative examples.
Understanding Complex Numbers
Before diving into the conjugate in polar form, let's refresh our understanding of complex numbers. A complex number z is typically represented in the rectangular or Cartesian form as:
z = a + bi
where:
- a is the real part (Re(z))
- b is the imaginary part (Im(z))
- i is the imaginary unit (√-1)
Polar Form of a Complex Number
The polar form offers an alternative representation, providing a geometric interpretation of complex numbers. It leverages the magnitude (or modulus) and argument (or angle) of the complex number.
z = r(cos θ + i sin θ)
where:
- r is the magnitude (or modulus) of z, calculated as: r = √(a² + b²)
- θ is the argument (or angle) of z, calculated as: θ = arctan(b/a) (Note: The arctan function needs careful consideration of the quadrant to ensure accuracy).
This form can be further simplified using Euler's formula:
e^(iθ) = cos θ + i sin θ
Therefore, the polar form can also be expressed as:
z = r e^(iθ)
The Conjugate of a Complex Number
The conjugate of a complex number z, denoted as z<sup>*</sup> or z̄, is obtained by changing the sign of the imaginary part. In rectangular form:
If z = a + bi, then z = a - bi*
Conjugate of a Complex Number in Polar Form: The Derivation
Now, let's derive the polar form of the conjugate. Starting with the polar form:
z = r(cos θ + i sin θ)
The conjugate, z*, is obtained by changing the sign of the imaginary part:
z = r(cos θ - i sin θ)*
Using Euler's formula, we can write this as:
z = r (cos(-θ) + i sin(-θ))*
Since cosine is an even function (cos(-θ) = cos θ) and sine is an odd function (sin(-θ) = -sin θ), we have:
z = r e^(-iθ)*
This elegantly shows that the conjugate in polar form simply involves negating the argument (angle) while keeping the magnitude the same.
Geometric Interpretation
Geometrically, the conjugate reflects the complex number across the real axis. If you plot z and z<sup>*</sup> on the complex plane, they will be mirror images of each other with respect to the real axis. The distance from the origin remains the same (r), only the angle changes its sign.
Properties of the Conjugate in Polar Form
The conjugate in polar form retains several essential properties:
- Magnitude: The magnitude of a complex number and its conjugate are equal: |z| = |z*| = r
- Argument: The argument of the conjugate is the negative of the argument of the original complex number: arg(z*) = -arg(z) = -θ
- Product: The product of a complex number and its conjugate is always a real number and equal to the square of its magnitude: z * z* = r²
- Sum and Difference: The sum of a complex number and its conjugate is twice the real part: z + z* = 2a. The difference is twice the imaginary part multiplied by i: z - z* = 2bi
Applications of the Conjugate in Polar Form
The conjugate of a complex number, particularly in its polar form, plays a critical role in numerous applications:
1. Division of Complex Numbers
Dividing complex numbers is often simplified using the conjugate. Multiplying both the numerator and denominator by the conjugate of the denominator eliminates the imaginary part from the denominator, making the result easier to interpret.
2. Finding Roots of Complex Numbers (De Moivre's Theorem)
De Moivre's Theorem utilizes the polar form and the properties of conjugates to efficiently find the nth roots of a complex number.
3. Signal Processing and Electrical Engineering
In these fields, complex numbers represent signals or impedances. The conjugate is used extensively in calculations involving power, impedance matching, and filter design. The concept of conjugate symmetry is crucial in understanding Fourier transforms and other signal processing techniques.
4. Quantum Mechanics
Complex numbers are fundamental to quantum mechanics, representing wave functions and quantum states. Conjugates are used in calculating probabilities and expectation values.
5. Solving Polynomial Equations
The conjugate pairs theorem states that if a polynomial with real coefficients has a complex root, its conjugate is also a root. This significantly aids in solving higher-order polynomial equations.
Examples
Let's illustrate these concepts with a few examples:
Example 1:
Let z = 2 + 2i.
- Rectangular Form: z = 2 + 2i
- Magnitude: r = √(2² + 2²) = √8 = 2√2
- Argument: θ = arctan(2/2) = π/4 (First quadrant)
- Polar Form: z = 2√2 (cos(π/4) + i sin(π/4)) or 2√2 e^(iπ/4)
- Conjugate (Rectangular): z* = 2 - 2i
- Conjugate (Polar): z* = 2√2 (cos(-π/4) + i sin(-π/4)) or 2√2 e^(-iπ/4)
Example 2:
Let z = 3e^(i(2π/3))
- Polar Form: z = 3e^(i(2π/3))
- Magnitude: r = 3
- Argument: θ = 2π/3
- Rectangular Form: z = 3(cos(2π/3) + i sin(2π/3)) = -3/2 + i(3√3/2)
- Conjugate (Polar): z* = 3e^(-i(2π/3))
- Conjugate (Rectangular): z* = 3(cos(-2π/3) + i sin(-2π/3)) = -3/2 - i(3√3/2)
Conclusion
The conjugate of a complex number in polar form provides a powerful tool for manipulating and understanding complex numbers geometrically and algebraically. Its properties and applications extend across numerous scientific and engineering disciplines. Understanding the relationship between the rectangular and polar forms of a complex number and its conjugate is crucial for mastering advanced mathematical and scientific concepts. By grasping the concepts detailed in this guide, you will be better equipped to tackle complex problems involving complex numbers. Remember to always consider the quadrant when calculating the argument to avoid ambiguity. Practice with different examples to solidify your understanding and appreciate the elegance and utility of this fundamental concept.
Latest Posts
Latest Posts
-
How Are Rhombuses And Squares Alike
May 09, 2025
-
What Are The Vertices Of A Triangle
May 09, 2025
-
In The Visible Spectrum What Color Has The Longest Wavelength
May 09, 2025
-
Which Of These Is A Male Gametophyte
May 09, 2025
-
What Are The Horizontal Columns On The Periodic Table Called
May 09, 2025
Related Post
Thank you for visiting our website which covers about Conjugate Of A Complex Number In Polar Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.