Common Multiples Of 9 And 7
Juapaving
Apr 08, 2025 · 5 min read
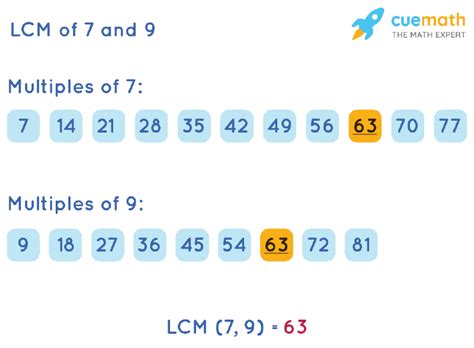
Table of Contents
Unveiling the Mysteries of Common Multiples: A Deep Dive into 9 and 7
Finding common multiples might seem like a simple arithmetic task, but understanding the underlying principles and exploring the nuances can unlock a deeper appreciation for number theory. This article delves into the fascinating world of common multiples, specifically focusing on the numbers 9 and 7. We'll unravel their intricacies, explore efficient methods for finding them, and even touch upon their applications in various fields. Prepare to embark on a numerical adventure!
Understanding Multiples and Common Multiples
Before we dive into the specifics of 9 and 7, let's establish a solid foundation. A multiple of a number is the product of that number and any integer. For example, multiples of 9 include 9 (9 x 1), 18 (9 x 2), 27 (9 x 3), and so on. Similarly, multiples of 7 include 7 (7 x 1), 14 (7 x 2), 21 (7 x 3), and so on.
A common multiple is a number that is a multiple of two or more numbers. In our case, we are looking for numbers that are multiples of both 9 and 7. These numbers share a special relationship, indicating a shared divisibility by both 9 and 7.
Finding the Least Common Multiple (LCM) of 9 and 7
The Least Common Multiple (LCM) is the smallest positive common multiple of two or more numbers. Finding the LCM is a crucial step in many mathematical operations, including simplifying fractions and solving problems related to cycles and periodic events.
There are several methods to find the LCM of 9 and 7:
Method 1: Listing Multiples
This is a straightforward approach, particularly useful for smaller numbers. We list the multiples of each number until we find a common one:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126...
Notice that 63 and 126 appear in both lists. Therefore, 63 is the least common multiple of 9 and 7. 126 is also a common multiple, but it's not the least.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We find the prime factorization of each number:
- 9 = 3 x 3 = 3²
- 7 = 7 (7 is a prime number)
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(9, 7) = 3² x 7 = 9 x 7 = 63
This method clearly shows that the LCM is 63.
Method 3: Using the Formula
There's a formula that relates the LCM and the Greatest Common Divisor (GCD) of two numbers:
LCM(a, b) = (|a x b|) / GCD(a, b)
The GCD of 9 and 7 is 1 (because they are coprime – they share no common factors other than 1). Therefore:
LCM(9, 7) = (9 x 7) / 1 = 63
This confirms our previous results.
Finding Other Common Multiples of 9 and 7
The LCM is just the smallest common multiple. To find other common multiples, we simply multiply the LCM by any positive integer:
- 63 x 1 = 63
- 63 x 2 = 126
- 63 x 3 = 189
- 63 x 4 = 252
- and so on...
Therefore, the set of common multiples of 9 and 7 is {63, 126, 189, 252, 315, ...}. This sequence continues infinitely.
Applications of Common Multiples
Understanding common multiples has practical applications in various fields:
Scheduling and Synchronization
Imagine two buses that depart from a station at regular intervals. One bus departs every 9 minutes, and the other every 7 minutes. Finding the common multiples helps determine when both buses will depart at the same time. The first time they'll depart together will be in 63 minutes (the LCM).
Pattern Recognition and Cycles
Common multiples are crucial in recognizing repeating patterns and cycles. In fields like music (rhythms and melodies) or even visual arts (repeating designs), understanding LCM helps predict the points where patterns coincide.
Fraction Operations
The LCM plays a vital role in adding and subtracting fractions with different denominators. To add 1/9 and 1/7, you need to find a common denominator, which is the LCM (63). This allows you to rewrite the fractions as 7/63 and 9/63, making the addition straightforward.
Exploring the Relationship Between 9 and 7
The numbers 9 and 7 are interesting because they are coprime, meaning their greatest common divisor (GCD) is 1. This implies they share no common factors other than 1. This coprime relationship significantly impacts their multiples; they don't share any common multiples smaller than their product. This property is unique and affects the behavior of their common multiples.
Their coprime nature simplifies calculations when finding the LCM. Since their GCD is 1, the LCM is simply their product (9 x 7 = 63). This simplification is not true for all number pairs.
Advanced Concepts and Extensions
The concepts discussed here can be extended to more than two numbers. Finding the LCM of three or more numbers involves similar techniques, but the complexity increases. Prime factorization becomes even more useful in these situations.
Furthermore, the study of common multiples extends into abstract algebra, where the concept is generalized to more complex mathematical structures.
Conclusion: The Enduring Significance of Common Multiples
Understanding common multiples, especially for numbers like 9 and 7, isn't merely an exercise in arithmetic. It's a gateway to appreciating the intricate relationships between numbers and their far-reaching applications. From scheduling problems to fraction simplification, the LCM and other common multiples form the foundation for solving numerous practical and theoretical problems across various disciplines. The seemingly simple concept of multiples unlocks a world of mathematical elegance and practical utility. This exploration serves as a reminder that even the most fundamental mathematical concepts have the power to illuminate our understanding of the world around us. So, next time you encounter common multiples, take a moment to appreciate the depth and breadth of this seemingly simple idea.
Latest Posts
Latest Posts
-
How Many Feet Is 65 In
Apr 08, 2025
-
5 Letter Words Beginning With Ae
Apr 08, 2025
-
The Most Abundant Metal In The Earths Crust Is
Apr 08, 2025
-
Log 1 2 3 Log1 Log2 Log3
Apr 08, 2025
-
How Many Valence Electrons Does Alkali Metals Have
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 9 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.