Common Multiple Of 28 And 98
Juapaving
Apr 04, 2025 · 5 min read
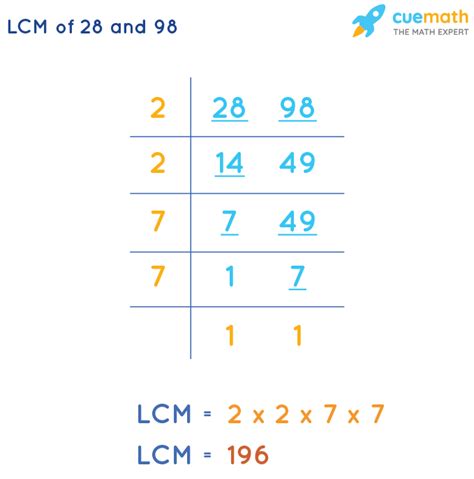
Table of Contents
Finding the Least Common Multiple (LCM) of 28 and 98: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications ranging from simple fraction arithmetic to complex scheduling problems. This article delves deep into the process of calculating the LCM of 28 and 98, exploring various methods and providing a thorough understanding of the underlying principles. We'll also examine the broader context of LCMs and their significance in mathematical problem-solving.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific problem of finding the LCM of 28 and 98, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both numbers divide into evenly.
For example, let's consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24, 28... and the multiples of 6 are 6, 12, 18, 24, 30... Notice that 12 and 24 are common multiples of both 4 and 6. However, 12 is the smallest of these common multiples, making it the least common multiple (LCM) of 4 and 6.
Methods for Finding the LCM of 28 and 98
Several methods exist for determining the LCM of two numbers. We will explore three common approaches: the listing method, the prime factorization method, and the greatest common divisor (GCD) method. Each method provides a valuable perspective on the concept of LCMs.
1. The Listing Method
This method involves listing the multiples of each number until a common multiple is found. While simple for smaller numbers, it becomes increasingly inefficient for larger numbers.
- Multiples of 28: 28, 56, 84, 112, 140, 168, 196, 224, 252, 280, 308, 336, 364, 392, 420, 448, 476, 504, 532, 560, 588, 616, 644, 672, 700, 728, 756, 784, 812, 840, 868, 896, 924, 952, 980...
- Multiples of 98: 98, 196, 294, 392, 490, 588, 686, 784, 882, 980...
By comparing the lists, we can see that 196, 392, 588, 784, and 980 are common multiples. The least of these is 196. Therefore, the LCM of 28 and 98 is 196. However, this method can be time-consuming and error-prone, especially with larger numbers.
2. The Prime Factorization Method
This method is generally more efficient than the listing method, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in either factorization.
Let's find the prime factorization of 28 and 98:
- 28 = 2² x 7¹
- 98 = 2¹ x 7²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- LCM(28, 98) = 2² x 7² = 4 x 49 = 196
This method provides a more systematic and reliable way to calculate the LCM, even for larger numbers.
3. The Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula connecting the LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 28 and 98. We can use the Euclidean algorithm for this:
- Divide 98 by 28: 98 = 28 x 3 + 14
- Divide 28 by 14: 28 = 14 x 2 + 0
The GCD is the last non-zero remainder, which is 14.
Now, we can use the formula:
LCM(28, 98) = (28 x 98) / GCD(28, 98) = (28 x 98) / 14 = 196
This method is also efficient and provides a clear mathematical relationship between the LCM and GCD.
Applications of LCMs
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses depart from a station at different intervals, the LCM helps determine when they will depart at the same time.
-
Fraction Arithmetic: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Gear Ratios: In mechanical engineering, LCMs are used to calculate gear ratios and synchronize rotating components.
-
Cyclic Processes: Analyzing repetitive events that occur at different intervals, such as the cyclical nature of certain astronomical phenomena.
Advanced Concepts and Extensions
The calculation of LCMs can be extended to more than two numbers. The principles remain the same, but the calculations become slightly more involved. For example, to find the LCM of three numbers, you would first find the LCM of two of them, and then find the LCM of that result and the third number.
The prime factorization method remains the most efficient approach for finding the LCM of multiple numbers. However, for very large numbers, specialized algorithms are employed to improve computational efficiency.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a crucial skill in mathematics with practical applications in diverse fields. The methods outlined in this article provide a comprehensive understanding of how to calculate the LCM, specifically for the numbers 28 and 98, but the principles can be applied to any pair of integers. Mastering these techniques empowers you to solve a wide range of mathematical problems and opens doors to understanding more complex concepts in various disciplines. Remember to choose the method that best suits your needs and the complexity of the numbers involved. Understanding the underlying principles of LCMs and the relationships between LCMs and GCDs is key to developing a strong mathematical foundation.
Latest Posts
Latest Posts
-
Class 10 History Ch 2 Notes
Apr 05, 2025
-
An Example Of An Oil In Water Emulsion Is
Apr 05, 2025
-
Ficks Law Of Diffusion Transcellular Pathway
Apr 05, 2025
-
What Is The Least Common Multiple Of 12 And 4
Apr 05, 2025
-
How Many Minutes Is 9 Hours
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Common Multiple Of 28 And 98 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
