Combine Like Terms 3x 2x 3y-7y
Juapaving
May 13, 2025 · 4 min read
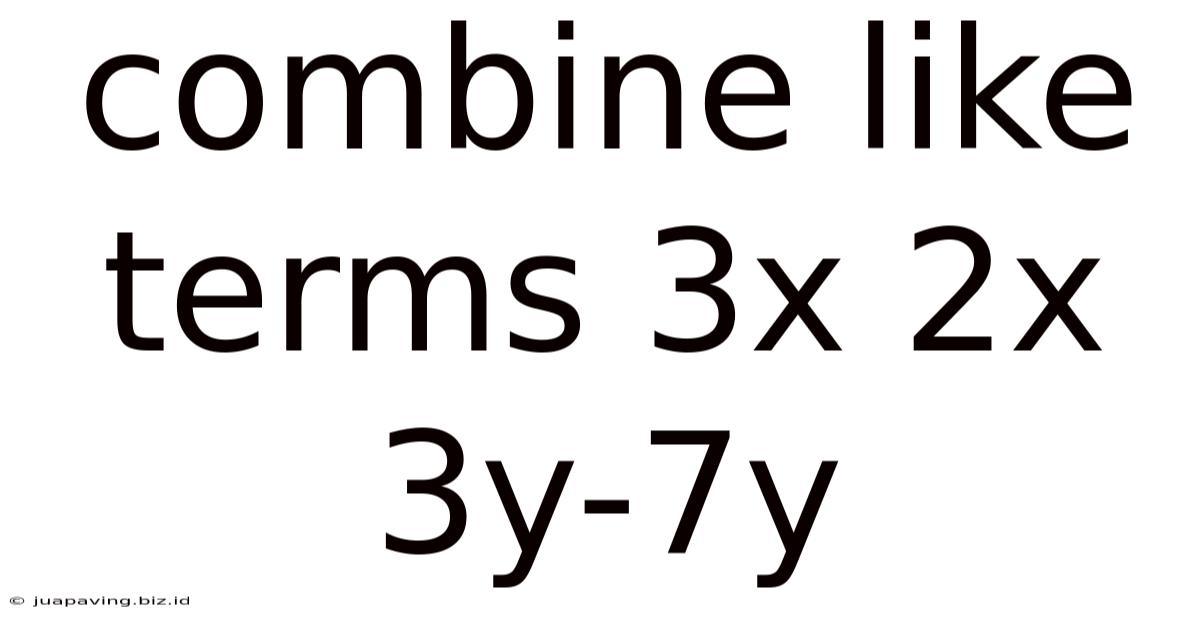
Table of Contents
Combining Like Terms: A Comprehensive Guide
Combining like terms is a fundamental concept in algebra, crucial for simplifying expressions and solving equations. This comprehensive guide will delve into the intricacies of combining like terms, providing a step-by-step approach, examples, and advanced applications to solidify your understanding. We'll specifically address the example expression, 3x + 2x + 3y - 7y, and expand upon the principles to handle more complex scenarios.
Understanding Like Terms
Before diving into the mechanics of combining like terms, it's essential to understand what constitutes a "like term." Like terms are terms that have the same variables raised to the same powers. Let's break this down:
- Variables: These are the letters (e.g., x, y, z) representing unknown quantities.
- Powers (Exponents): These indicate how many times a variable is multiplied by itself (e.g., x², y³, z). If a variable doesn't have a visible exponent, it's understood to be raised to the power of 1 (e.g., x = x¹).
Examples of Like Terms:
3xand2x(same variable, x, raised to the power of 1)5y²and-2y²(same variable, y, raised to the power of 2)-7aband4ab(same variables, a and b, each raised to the power of 1)
Examples of Unlike Terms:
3xand3y(different variables)2x²and2x(same variable but different powers)4aband4a²b(same variables but different powers)
Combining Like Terms: The Process
Combining like terms involves adding or subtracting the coefficients (the numbers in front of the variables) of the like terms. The variable part remains unchanged.
Let's illustrate this with our example expression: 3x + 2x + 3y - 7y
-
Identify Like Terms: We have two sets of like terms:
3xand2x3yand-7y
-
Combine Coefficients:
- For the 'x' terms: 3 + 2 = 5. So,
3x + 2xsimplifies to5x. - For the 'y' terms: 3 + (-7) = -4. So,
3y - 7ysimplifies to-4y.
- For the 'x' terms: 3 + 2 = 5. So,
-
Write the Simplified Expression: Combining the simplified terms, we get:
5x - 4y.
Therefore, 3x + 2x + 3y - 7y = 5x - 4y. This is the simplest form of the expression because we cannot combine 5x and -4y further; they are unlike terms.
More Complex Examples
Let's tackle more challenging examples to solidify your understanding:
Example 1:
4a²b + 2ab² - 3a²b + 5ab²
-
Identify Like Terms:
4a²band-3a²b2ab²and5ab²
-
Combine Coefficients:
4a²b - 3a²b = a²b2ab² + 5ab² = 7ab²
-
Simplified Expression:
a²b + 7ab²
Example 2:
5x³ - 2x² + 7x - 3x³ + 4x² - 2x
-
Identify Like Terms:
5x³and-3x³-2x²and4x²7xand-2x
-
Combine Coefficients:
5x³ - 3x³ = 2x³-2x² + 4x² = 2x²7x - 2x = 5x
-
Simplified Expression:
2x³ + 2x² + 5x
Example 3: Incorporating Parentheses
2(x + 3y) - 4(2x - y)
-
Distribute: First, distribute the numbers outside the parentheses to the terms inside:
2(x + 3y) = 2x + 6y-4(2x - y) = -8x + 4y
-
Combine Like Terms:
2x - 8x = -6x6y + 4y = 10y
-
Simplified Expression:
-6x + 10y
Applications of Combining Like Terms
Combining like terms is not just an algebraic exercise; it's a crucial skill applied extensively in various mathematical and real-world contexts:
- Solving Equations: Simplifying equations by combining like terms makes them easier to solve.
- Geometry: Calculating perimeters and areas often involves combining like terms.
- Physics: Many physics formulas require manipulating algebraic expressions, including combining like terms.
- Data Analysis: Simplifying complex data representations frequently involves this process.
Common Mistakes to Avoid
While combining like terms seems straightforward, certain errors can occur:
- Combining Unlike Terms: This is the most common mistake. Remember, only like terms can be combined.
- Incorrectly Combining Coefficients: Pay close attention to the signs (+ or -) of the coefficients.
- Forgetting to Distribute: When dealing with parentheses, ensure that you correctly distribute the term outside the parentheses to every term inside.
Advanced Techniques and Further Exploration
Once you've mastered the basics, consider these advanced concepts:
- Polynomial Operations: Combining like terms is fundamental to adding, subtracting, multiplying, and dividing polynomials.
- Factoring: After combining like terms, you can often factor the simplified expression to further reduce it.
- Solving Systems of Equations: Combining like terms plays a vital role in solving systems of equations using methods like elimination.
Conclusion
Combining like terms is a fundamental algebraic skill that simplifies expressions, leading to more efficient problem-solving. By understanding like terms, mastering the combining process, and avoiding common mistakes, you'll build a strong foundation in algebra and its numerous applications. Remember to practice regularly with diverse examples to refine your skills and build confidence. This comprehensive guide provides a solid starting point for your journey into the world of algebraic simplification. Continue exploring advanced concepts to further enhance your mathematical proficiency.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 24 And 9
May 13, 2025
-
The Portrait Of A Lady Summary
May 13, 2025
-
Greatest Common Factor Of 18 And 42
May 13, 2025
-
Sbi New Passbook Application Form Pdf
May 13, 2025
-
First 36 Elements Of Periodic Table
May 13, 2025
Related Post
Thank you for visiting our website which covers about Combine Like Terms 3x 2x 3y-7y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.