By How Much Does 1 Exceed 2x 3y 4
Juapaving
May 11, 2025 · 5 min read
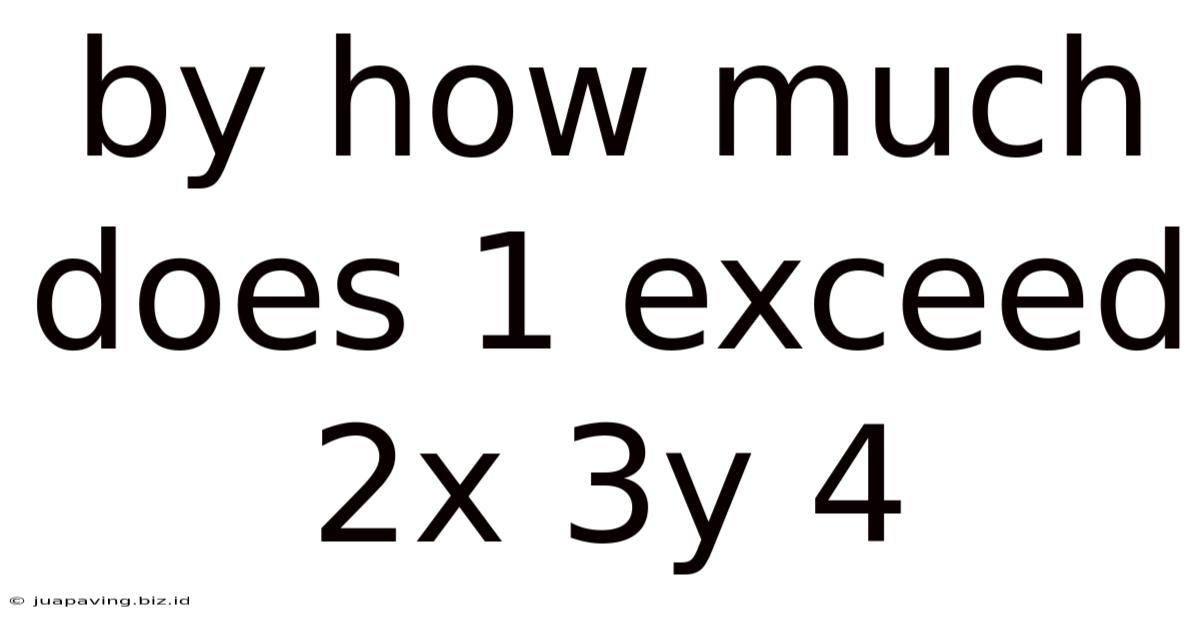
Table of Contents
By How Much Does 1 Exceed 2x + 3y + 4? A Deep Dive into Algebraic Expressions
The seemingly simple question, "By how much does 1 exceed 2x + 3y + 4?" unveils a rich tapestry of algebraic concepts. While the immediate answer might seem straightforward, a deeper exploration reveals opportunities to discuss fundamental mathematical principles, problem-solving strategies, and the importance of precise mathematical language. This article will delve into this seemingly simple problem, unpacking its intricacies and showcasing its relevance in various mathematical contexts.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in understanding the phrase "exceed." In mathematical terms, "A exceeds B" means that A is greater than B. The difference between A and B represents the amount by which A exceeds B. Therefore, our question translates to finding the difference between 1 and the expression 2x + 3y + 4. This difference will be represented by a new algebraic expression.
Key Terms and Definitions:
- Algebraic Expression: A combination of variables (like x and y), constants (like 1, 2, 3, 4), and mathematical operations (+, -, ×, ÷).
- Variable: A symbol (usually a letter) representing an unknown quantity.
- Constant: A fixed numerical value.
- Difference: The result of subtracting one number or expression from another.
Solving the Problem: Finding the Difference
To find by how much 1 exceeds 2x + 3y + 4, we need to perform a subtraction:
1 - (2x + 3y + 4)
This subtraction involves distributing the negative sign to each term within the parentheses:
1 - 2x - 3y - 4
Now, we combine like terms (constants in this case):
(1 - 4) - 2x - 3y
This simplifies to:
-3 - 2x - 3y
Therefore, 1 exceeds 2x + 3y + 4 by -3 - 2x - 3y.
This result is an algebraic expression itself. Its value depends on the specific values assigned to the variables x and y.
Exploring Different Scenarios and Interpretations
The expression -3 - 2x - 3y offers several avenues for further exploration:
Scenario 1: x = 0, y = 0
If x = 0 and y = 0, the expression becomes:
-3 - 2(0) - 3(0) = -3
In this case, 1 exceeds 2x + 3y + 4 by -3. This means that 2x + 3y + 4 is actually greater than 1.
Scenario 2: x = -1, y = -1
If x = -1 and y = -1, the expression becomes:
-3 - 2(-1) - 3(-1) = -3 + 2 + 3 = 2
Here, 1 exceeds 2x + 3y + 4 by 2. Again, 2x + 3y + 4 is less than 1.
Scenario 3: Finding Values Where 1 = 2x + 3y + 4
We can also investigate the conditions under which 1 equals 2x + 3y + 4. This would mean the difference between 1 and 2x + 3y + 4 is zero. This leads to the equation:
1 = 2x + 3y + 4
Subtracting 1 from both sides gives:
0 = 2x + 3y + 3
This equation represents a line in the xy-plane. Any point (x, y) on this line satisfies the condition where 1 does not exceed 2x + 3y + 4; instead, they are equal.
The Importance of Mathematical Precision and Notation
This seemingly simple problem highlights the importance of precise mathematical language and notation. The seemingly ambiguous phrasing "by how much does 1 exceed..." requires careful interpretation to ensure the correct mathematical operation is performed. The use of parentheses in the subtraction is crucial to avoid errors in the sign of the terms.
Applications in Real-World Scenarios
While this problem may appear abstract, it has practical applications in various fields:
- Finance: Imagine calculating profit (1) where costs (2x + 3y + 4) are represented by variables. The expression -3 - 2x - 3y represents the profit margin, which can be positive or negative depending on the values of x and y (costs).
- Engineering: In design and construction, algebraic expressions are used to model relationships between different variables. This problem’s methodology could be used to analyze differences in expected outcomes and actual results.
- Physics: Many physical phenomena are modeled using algebraic equations. Determining the difference between a theoretical value (1) and an experimental measurement (2x + 3y + 4) is crucial for evaluating the accuracy of the model.
Expanding the Concepts: Further Exploration
This basic problem can be expanded to explore more complex concepts:
- Inequalities: Instead of finding the exact difference, we could investigate when 1 exceeds 2x + 3y + 4 (1 > 2x + 3y + 4) or when 2x + 3y + 4 exceeds 1 (2x + 3y + 4 > 1). This leads to the study of inequalities and their graphical representations.
- Systems of Equations: If we had additional equations involving x and y, we could solve a system of equations to find specific values of x and y that satisfy those equations and then substitute them into our difference expression.
- Calculus: In calculus, the concept of limits allows us to analyze the behavior of expressions as variables approach specific values or infinity.
Conclusion: The Power of Simplicity
The question of how much 1 exceeds 2x + 3y + 4, while initially simple, reveals the power of algebraic manipulation and the importance of precise mathematical thinking. It provides a stepping stone to more complex mathematical concepts, highlighting the practical applications of algebra in various fields. By understanding this seemingly basic problem, we gain a deeper appreciation for the elegance and utility of mathematics. The exploration of different scenarios and the manipulation of algebraic expressions offer valuable insights into problem-solving techniques and the importance of clarity in mathematical communication. Furthermore, the ability to interpret and apply this knowledge to real-world scenarios underscores the relevance of mathematical principles in practical applications.
Latest Posts
Latest Posts
-
Can A Convex Mirror Form A Real Image
May 14, 2025
-
5 Letter Word Starts With Pen
May 14, 2025
-
The Primary Pacemaker Of The Heart Is The
May 14, 2025
-
Which Of The Following Are Directly Associated With Photosystem I
May 14, 2025
-
How Do You Multiply Mixed Fractions With A Whole Number
May 14, 2025
Related Post
Thank you for visiting our website which covers about By How Much Does 1 Exceed 2x 3y 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.