Bar That Is Free To Pivot About A Fixed Point
Juapaving
Apr 04, 2025 · 6 min read
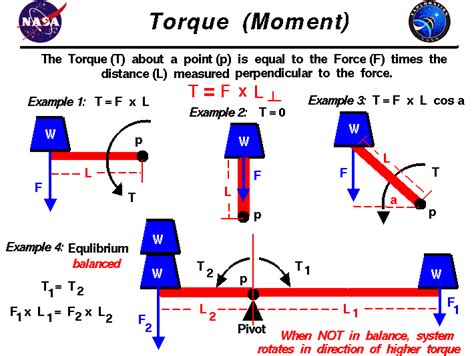
Table of Contents
A Bar Free to Pivot About a Fixed Point: Exploring Rotational Dynamics
A rigid bar, free to pivot about a fixed point, represents a fundamental concept in classical mechanics with wide-ranging applications in engineering, physics, and beyond. Understanding its behavior, governed by principles of rotational dynamics, is crucial for analyzing various systems, from simple levers and seesaws to complex robotic arms and gyroscopes. This article delves into the intricacies of such a system, examining its motion, the forces acting upon it, and the mathematical tools used to describe its behavior.
Understanding the System: Defining the Parameters
Before we delve into the dynamics, let's clearly define our system. We are considering a rigid bar, meaning its shape and dimensions remain constant throughout its motion. This bar is free to rotate about a single, fixed point – often referred to as the pivot point or fulcrum. This pivot point restricts linear motion but allows for unrestricted rotational motion in a plane.
Several key parameters define the system's behavior:
- Mass (m): The total mass of the bar, influencing its inertia.
- Length (L): The length of the bar, impacting the moment of inertia and lever arm.
- Moment of Inertia (I): A measure of the bar's resistance to rotational acceleration. For a uniform bar rotating about its center, I = (1/12)mL². If the pivot point is at one end, I = (1/3)mL². The moment of inertia depends on the mass distribution and the axis of rotation.
- Angular Velocity (ω): The rate of change of the bar's angular displacement (θ), representing how fast the bar is rotating.
- Angular Acceleration (α): The rate of change of the angular velocity, indicating the bar's rotational acceleration.
- Torque (τ): The rotational equivalent of force, causing the bar to rotate. It's the product of force and the perpendicular distance from the pivot point to the line of action of the force (lever arm). Mathematically, τ = rFsinθ, where r is the lever arm, F is the force, and θ is the angle between r and F.
Newton's Second Law for Rotation: Governing the Motion
The motion of the bar is governed by Newton's second law for rotation, a direct analog to the linear version (F=ma):
τ = Iα
This equation states that the net torque acting on the bar is directly proportional to its angular acceleration and is dependent on its moment of inertia. A larger torque leads to a greater angular acceleration, while a larger moment of inertia implies a greater resistance to angular acceleration.
Understanding this equation is critical. If the net torque on the bar is zero, then the angular acceleration is zero, and the bar will either remain stationary or rotate at a constant angular velocity (due to inertia). If a non-zero net torque acts, the bar will experience angular acceleration, changing its rotational speed.
Forces and Torques Acting on the Bar
Several forces can act on the bar, each contributing to the net torque:
- Gravitational Force: The weight of the bar acts downwards at its center of mass. This creates a torque unless the center of mass lies directly on the pivot point.
- Applied Forces: External forces applied to the bar at any point will produce a torque about the pivot point. The magnitude and direction of this torque depend on the force's magnitude, direction, and its distance from the pivot.
- Frictional Forces: Friction at the pivot point can oppose rotation, creating a torque opposing the motion. This is often neglected in idealized models but becomes significant in real-world scenarios.
Solving Problems Involving Rotating Bars
Many problems involve determining the angular acceleration, angular velocity, or angular displacement of the bar given specific forces and initial conditions. Here's a breakdown of the problem-solving approach:
-
Free Body Diagram: Draw a free body diagram showing all forces acting on the bar and their points of application.
-
Torque Calculation: Calculate the torque produced by each force about the pivot point. Remember that torque is a vector quantity; consider its direction (clockwise or counterclockwise).
-
Net Torque: Determine the net torque by summing the individual torques, considering their directions.
-
Newton's Second Law for Rotation: Apply the equation τ = Iα to find the angular acceleration.
-
Kinematics Equations: Use the kinematic equations for rotational motion to find the angular velocity and angular displacement as a function of time. These equations are analogous to their linear counterparts:
- ω = ω₀ + αt
- θ = ω₀t + (1/2)αt²
- ω² = ω₀² + 2αθ
where ω₀ is the initial angular velocity.
Real-world Applications
The concept of a bar free to pivot about a fixed point finds numerous applications in various fields:
- Levers and Seesaws: These simple machines utilize the principle of torque balance to amplify force or create mechanical advantage.
- Balances and Scales: Precise measurement of mass relies on the balance of torques produced by the unknown mass and known weights.
- Robotic Arms: Complex robotic systems use multiple rotating bars (links) to achieve precise movements. Understanding the rotational dynamics of each link is crucial for controlling the arm's motion.
- Gyroscopes: These devices utilize the principle of conservation of angular momentum to maintain orientation, crucial in navigation systems and stabilizing platforms.
- Doors and Hinges: The rotation of a door about its hinges is a simple example of this concept.
- Gears and Gear Trains: The meshing of gears involves the transfer of rotational motion between bars, relying on the principles of torque and rotational kinematics.
Advanced Concepts and Considerations
While the basic principles outlined above provide a strong foundation, several advanced concepts can further enhance understanding:
- Non-uniform Bars: For bars with non-uniform mass distribution, the moment of inertia calculation becomes more complex, requiring integration techniques.
- Multiple Forces: Analyzing systems with multiple forces requires careful consideration of the net torque and its effect on the bar's motion.
- Energy Considerations: The conservation of energy can be applied to analyze the bar's motion, relating its kinetic energy of rotation to the work done by external forces.
- Damped Oscillations: In real-world systems, friction and other dissipative forces can cause damped oscillatory motion.
Conclusion
The seemingly simple system of a bar free to pivot about a fixed point provides a rich foundation for understanding rotational dynamics. Mastering the concepts of torque, moment of inertia, and Newton's second law for rotation allows for the analysis and prediction of the behavior of numerous mechanical systems. From simple levers to complex robotic arms, the principles discussed in this article are essential for engineers, physicists, and anyone seeking a deeper understanding of the physical world. Further exploration into advanced concepts such as non-uniform mass distribution, energy considerations, and damped oscillations can unlock even more sophisticated applications and deepen your understanding of this fundamental principle in mechanics.
Latest Posts
Latest Posts
-
800 Sq M To Sq Ft
Apr 04, 2025
-
Does A Parallelogram Have One Pair Of Parallel Sides
Apr 04, 2025
-
Algebraic Expressions Class 7 Practice Questions
Apr 04, 2025
-
What Is The Least Common Multiple Of 7 And 12
Apr 04, 2025
-
Base And Exponent Pdf With Answers 7th
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Bar That Is Free To Pivot About A Fixed Point . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
