Area Moment Of Inertia Of A Triangle
Juapaving
Apr 01, 2025 · 6 min read
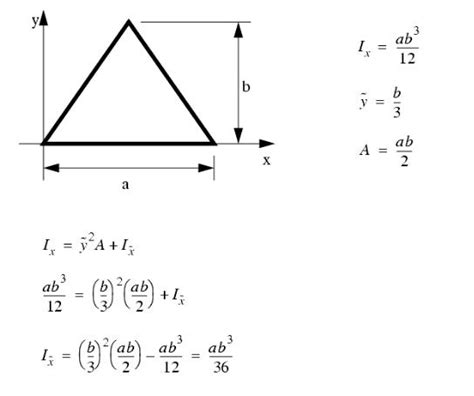
Table of Contents
Area Moment of Inertia of a Triangle: A Comprehensive Guide
The area moment of inertia, also known as the second moment of area, is a crucial concept in engineering and physics, particularly in structural analysis and mechanics of materials. It quantifies how the area of a cross-section is distributed relative to a given axis. Understanding this concept is vital for calculating bending stresses, deflections, and overall structural stability. This comprehensive guide will delve into the area moment of inertia of a triangle, exploring its calculation methods, applications, and practical implications.
What is the Area Moment of Inertia?
Before we dive into the specifics of triangles, let's establish a foundational understanding of the area moment of inertia. It represents the resistance of a cross-sectional area to bending or flexing about a specific axis. The further the area is located from the axis, the greater its contribution to the moment of inertia. This is because the moment of inertia is calculated by summing the product of each infinitesimal area element and the square of its distance from the axis. Mathematically, it's represented as:
I<sub>x</sub> = ∫ y<sup>2</sup> dA
Where:
- I<sub>x</sub> is the area moment of inertia about the x-axis.
- y is the perpendicular distance from the infinitesimal area element (dA) to the x-axis.
- dA is an infinitesimal area element.
Similarly, for the y-axis:
I<sub>y</sub> = ∫ x<sup>2</sup> dA
And for the polar moment of inertia (about an axis perpendicular to the plane):
J = I<sub>x</sub> + I<sub>y</sub> = ∫ (x<sup>2</sup> + y<sup>2</sup>) dA
Calculating the Area Moment of Inertia for a Triangle
Calculating the area moment of inertia for a triangle can be approached using various methods, including integration and using established formulas. The complexity of the calculation depends on the chosen axis and the triangle's orientation. We'll explore both approaches.
Method 1: Integration
The most fundamental approach is through integration. Let's consider a right-angled triangle with base 'b' and height 'h'. We'll derive the moment of inertia about the base (x-axis). The equation of the line forming the hypotenuse is y = (h/b)x.
We can express the infinitesimal area element as: dA = y dx
Now, substituting into the formula for I<sub>x</sub>:
I<sub>x</sub> = ∫<sub>0</sub><sup>b</sup> y<sup>2</sup> dA = ∫<sub>0</sub><sup>b</sup> y<sup>2</sup> (y dx) = ∫<sub>0</sub><sup>b</sup> y<sup>3</sup> dx
Substituting y = (h/b)x:
I<sub>x</sub> = ∫<sub>0</sub><sup>b</sup> ((h/b)x)<sup>3</sup> dx = (h<sup>3</sup>/b<sup>3</sup>) ∫<sub>0</sub><sup>b</sup> x<sup>3</sup> dx
Integrating and applying the limits:
I<sub>x</sub> = (h<sup>3</sup>/b<sup>3</sup>) [x<sup>4</sup>/4]<sub>0</sub><sup>b</sup> = (bh<sup>3</sup>)/12
This formula gives the area moment of inertia of a right-angled triangle about its base.
Method 2: Using Established Formulas
For various axes and triangle orientations, established formulas simplify the calculation. For a triangle with base 'b' and height 'h':
-
About the base (centroidal axis parallel to the base): I<sub>x</sub> = (bh<sup>3</sup>)/36
-
About an axis through the centroid parallel to the base: I<sub>x</sub> = (bh<sup>3</sup>)/36
-
About an axis through the vertex parallel to the base: I<sub>x</sub> = (bh<sup>3</sup>)/12
-
About an axis through the centroid parallel to the height: I<sub>y</sub> = (hb<sup>3</sup>)/36
-
About an axis through one side of the triangle and parallel to it: I = (1/12)l*t^3 where l is length of the side and t is thickness perpendicular to the side.
It is crucial to understand that the location of the reference axis significantly impacts the calculated moment of inertia. The formulas above assume specific axis locations.
Parallel Axis Theorem
The parallel axis theorem is a powerful tool used to calculate the area moment of inertia about any parallel axis, given the moment of inertia about a centroidal axis. It states:
I<sub>axis</sub> = I<sub>centroid</sub> + A * d<sup>2</sup>
Where:
- I<sub>axis</sub> is the moment of inertia about the desired axis.
- I<sub>centroid</sub> is the moment of inertia about the centroidal axis (parallel to the desired axis).
- A is the area of the shape.
- d is the distance between the centroidal axis and the desired axis.
Applications of Area Moment of Inertia of a Triangle
The area moment of inertia of a triangle, alongside the parallel axis theorem, finds wide applications in various engineering disciplines:
-
Structural Analysis: Calculating bending stresses and deflections in beams with triangular cross-sections. This is critical in designing structures such as bridges, trusses, and building frameworks where triangular components are frequently employed.
-
Mechanics of Materials: Determining the stiffness and strength of structural elements. A higher moment of inertia indicates greater resistance to bending.
-
Civil Engineering: Designing retaining walls and other structures that rely on the stability and strength of triangular elements.
-
Aerospace Engineering: Analyzing the load-bearing capacity of aircraft components, including wings and fuselage elements that might incorporate triangular shapes.
Practical Considerations and Examples
Let's illustrate the application with a few practical examples:
Example 1: A triangular beam with base 10 cm and height 5 cm is subjected to a bending moment. Calculate the moment of inertia about its base.
Using the formula I<sub>x</sub> = (bh<sup>3</sup>)/12, we get:
I<sub>x</sub> = (10 cm * (5 cm)<sup>3</sup>)/12 = 104.17 cm<sup>4</sup>
Example 2: Consider the same triangular beam. Calculate the moment of inertia about its centroidal axis parallel to the base.
Using the formula I<sub>x</sub> = (bh<sup>3</sup>)/36, we get:
I<sub>x</sub> = (10 cm * (5 cm)<sup>3</sup>)/36 = 26.04 cm<sup>4</sup>
Example 3: Applying the parallel axis theorem: Let's calculate the moment of inertia of the same triangular beam about an axis parallel to the base and located 2cm above the base. The distance between the centroidal axis and the new axis (d) is 2 cm + (5cm/3) = 5.67 cm. Centroidal moment of inertia was calculated to be 26.04 cm<sup>4</sup> above. The area is (1/2)(10cm)(5cm) = 25 cm<sup>2</sup>.
Using the parallel axis theorem:
I<sub>axis</sub> = 26.04 cm<sup>4</sup> + (25 cm<sup>2</sup>) * (5.67 cm)<sup>2</sup> = 831.68 cm<sup>4</sup>
Conclusion
The area moment of inertia of a triangle is a fundamental concept in engineering that dictates a structure's resistance to bending. Understanding how to calculate it, using both integration and established formulas, along with the application of the parallel axis theorem, is vital for accurate structural analysis and design. The examples provided illustrate the practical significance of this concept in real-world engineering applications. Furthermore, mastering this concept lays a strong foundation for tackling more complex shapes and structural scenarios. Remember that the selection of the appropriate axis and the application of the parallel axis theorem are crucial steps for obtaining accurate results. With careful consideration of these factors, engineers can ensure the structural integrity and stability of a wide range of structures.
Latest Posts
Latest Posts
-
Which Statements Are True Regarding Undefinable Terms In Geometry
Apr 02, 2025
-
What Is 3 Of 1 Million
Apr 02, 2025
-
In What Cell Organelle Does Photosynthesis Occur
Apr 02, 2025
-
Name 3 Kinds Of Hard Part Fossils
Apr 02, 2025
-
Convert 100 Degrees Celsius To Fahrenheit
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Area Moment Of Inertia Of A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
