Are Opposite Angles Of A Rhombus Congruent
Juapaving
Mar 28, 2025 · 6 min read
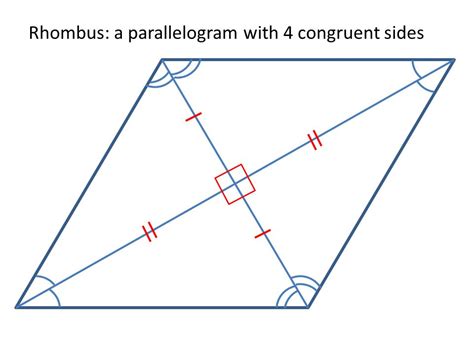
Table of Contents
Are Opposite Angles of a Rhombus Congruent? A Deep Dive into Rhombus Geometry
Are opposite angles of a rhombus congruent? The short answer is yes. This fundamental property of rhombuses is crucial to understanding their geometric characteristics and solving related problems. This article delves deep into the proof of this property, explores related concepts, and provides examples to solidify your understanding. We'll examine the rhombus's properties, explore its relationship to other quadrilaterals, and discuss its applications in various fields.
Understanding the Rhombus: A Unique Quadrilateral
Before diving into the proof, let's define what a rhombus is. A rhombus is a quadrilateral (a four-sided polygon) with all four sides having equal length. This characteristic distinguishes it from other quadrilaterals like squares, rectangles, and parallelograms. While a square is a special type of rhombus (with right angles), a rhombus doesn't necessarily have right angles. This seemingly small difference leads to important geometric distinctions.
Key Properties of a Rhombus
A rhombus boasts several key properties, some of which are directly related to its angles:
- Equilateral Sides: All four sides are congruent (equal in length). This is the defining characteristic of a rhombus.
- Opposite Sides are Parallel: Opposite sides are parallel to each other. This is a property it shares with parallelograms.
- Opposite Angles are Congruent: This is the core focus of this article. Opposite angles in a rhombus are always equal in measure.
- Consecutive Angles are Supplementary: Any two angles that share a side add up to 180 degrees.
- Diagonals Bisect Each Other: The diagonals of a rhombus intersect at a point, bisecting each other (cutting each other in half).
- Diagonals are Perpendicular Bisectors: The diagonals are perpendicular to each other, and each diagonal bisects the opposite angles.
Proving the Congruence of Opposite Angles
The congruence of opposite angles in a rhombus can be proven using several different approaches. We will explore two common methods:
Method 1: Using Parallelogram Properties
Since a rhombus is a special type of parallelogram (a quadrilateral with opposite sides parallel), we can leverage the properties of parallelograms to prove the congruence of opposite angles.
-
Parallelogram Property: In any parallelogram, opposite angles are congruent.
-
Rhombus as a Parallelogram: A rhombus is a parallelogram. This means it inherits all the properties of a parallelogram, including the congruence of opposite angles.
-
Conclusion: Therefore, opposite angles in a rhombus are congruent.
This method provides a concise and elegant proof, leveraging the established properties of parallelograms.
Method 2: Using Triangle Congruence
This method involves dividing the rhombus into two congruent triangles and demonstrating the congruence of corresponding angles.
-
Draw the Diagonals: Draw both diagonals of the rhombus. These diagonals divide the rhombus into four congruent triangles.
-
Consider Two Triangles: Focus on two triangles that share a common side (a diagonal). Let's call these triangles ΔABC and ΔADC, where AC is the diagonal.
-
Side-Side-Side (SSS) Congruence: We know that AB = BC = CD = DA (all sides of the rhombus are equal). Also, AC is a common side to both triangles. Therefore, by the SSS congruence postulate, ΔABC ≅ ΔADC.
-
Congruent Angles: Because the triangles are congruent, their corresponding angles are congruent. This means ∠ABC ≅ ∠ADC (opposite angles).
-
Repeat for Other Opposite Angles: The same process can be repeated using the other diagonal to prove that ∠BAD ≅ ∠BCD.
-
Conclusion: Therefore, opposite angles in a rhombus are congruent.
This method provides a more geometrically intuitive proof, relying on the fundamental concept of triangle congruence.
Relationship to Other Quadrilaterals
Understanding the relationship between a rhombus and other quadrilaterals is crucial to appreciate its unique properties.
-
Square: A square is a special case of a rhombus where all angles are right angles (90 degrees). Squares possess all the properties of a rhombus and more.
-
Rectangle: A rectangle is a quadrilateral with four right angles, but its sides don't necessarily have equal lengths. While a rhombus and a rectangle share the property of having opposite angles congruent, they differ significantly in side lengths.
-
Parallelogram: A rhombus is a special case of a parallelogram, inheriting all parallelogram properties but adding the constraint of equal side lengths. This explains why opposite angles are congruent in a rhombus (as they are in parallelograms).
-
Kite: A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. Unlike a rhombus, a kite does not necessarily have congruent opposite angles. Only one pair of opposite angles is congruent in a kite.
Applications of Rhombus Properties
The properties of a rhombus, particularly the congruence of its opposite angles, have applications in various fields:
-
Engineering: The stability and strength of rhombus-shaped structures are utilized in bridge construction, building frameworks, and other engineering projects. Understanding the angular properties is vital for structural integrity calculations.
-
Architecture: Rhombus shapes are used aesthetically in architectural designs, creating visually appealing and structurally sound buildings and spaces. The symmetry inherent in the congruent opposite angles adds to the design's balance.
-
Computer Graphics: In computer graphics and animation, understanding rhombus geometry is essential for creating precise shapes, generating textures, and implementing transformations in two-dimensional and three-dimensional modeling.
-
Tessellations: Rhombuses are frequently used in creating tessellations (patterns that cover a plane without overlaps or gaps). Their equal sides and congruent opposite angles make them particularly suitable for creating aesthetically pleasing and mathematically consistent patterns.
Solving Problems Involving Rhombus Angles
Let's consider a few examples to illustrate the practical application of the congruent opposite angles property:
Example 1:
A rhombus has one angle measuring 70 degrees. What are the measures of the other three angles?
- Solution: Since opposite angles are congruent, another angle will also measure 70 degrees. Consecutive angles are supplementary, meaning they add up to 180 degrees. Therefore, the other two angles will each measure 180 - 70 = 110 degrees.
Example 2:
The diagonals of a rhombus are given as 12 cm and 16 cm. Find the measures of all angles in the rhombus.
- Solution: The diagonals of a rhombus bisect each other at a right angle. This creates four right-angled triangles within the rhombus. Using trigonometry, we can calculate the angles formed by the diagonals and then use the supplementary angle property to find all the angles of the rhombus.
Example 3:
A rhombus is inscribed in a circle. What can you conclude about the rhombus?
- Solution: Only a square (a special type of rhombus) can be inscribed in a circle. This is because all angles of a square are 90 degrees, which is required for the vertices to lie on the circumference of a circle. A general rhombus with angles other than 90 degrees cannot be inscribed in a circle.
Conclusion
The congruence of opposite angles is a fundamental and essential property of a rhombus. This property, along with other defining characteristics, distinguishes the rhombus from other quadrilaterals and highlights its unique geometric features. Understanding this property is key to solving a wide range of geometric problems and appreciating the rhombus's significance in various fields, from engineering and architecture to computer graphics and art. Through the provided proofs and examples, we have demonstrated conclusively that opposite angles of a rhombus are indeed congruent, solidifying this critical geometric concept. Mastering this property paves the way for further exploration of more advanced geometric concepts and applications.
Latest Posts
Latest Posts
-
Greater Than Less Than Decimals Calculator
Mar 31, 2025
-
Father Of The Constitution Of India
Mar 31, 2025
-
Whats The Roman Numeral For 35
Mar 31, 2025
-
What Is 1 In 4 As A Percentage
Mar 31, 2025
-
Nouns That Start With A C
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Are Opposite Angles Of A Rhombus Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
