An Angle With A Measure Less Than 90 Degrees
Juapaving
May 10, 2025 · 6 min read
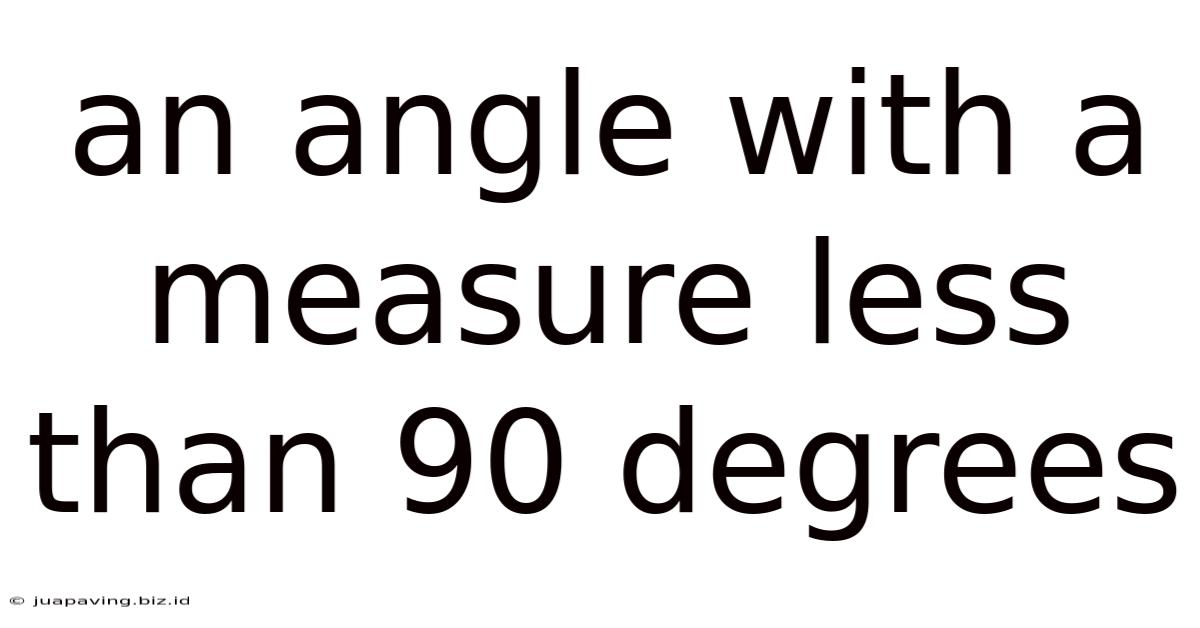
Table of Contents
An Angle with a Measure Less Than 90 Degrees: A Comprehensive Exploration of Acute Angles
An angle with a measure less than 90 degrees is called an acute angle. This seemingly simple geometric concept forms the foundation for countless mathematical and real-world applications. Understanding acute angles is crucial for anyone studying geometry, trigonometry, or any field that involves spatial reasoning. This comprehensive guide delves deep into the definition, properties, applications, and related concepts of acute angles.
Defining Acute Angles: The Fundamentals
In geometry, an angle is formed by two rays sharing a common endpoint, called the vertex. These rays are often referred to as the sides of the angle. Angles are measured in degrees, with a full circle encompassing 360 degrees. An acute angle is specifically defined as an angle whose measure is greater than 0 degrees and less than 90 degrees. This means it falls within the range of (0°, 90°).
It's crucial to differentiate acute angles from other types of angles:
- Right Angle: Measures exactly 90 degrees. Represented by a small square at the vertex.
- Obtuse Angle: Measures greater than 90 degrees but less than 180 degrees.
- Straight Angle: Measures exactly 180 degrees, forming a straight line.
- Reflex Angle: Measures greater than 180 degrees but less than 360 degrees.
Visualizing Acute Angles: Real-World Examples
Understanding acute angles becomes easier with real-world examples. Look around you! Acute angles are everywhere:
- The point of a pencil: The angle formed by the lead and the body of a sharpened pencil is typically acute.
- The hands of a clock: At most times, the hands of a clock form an acute angle. For example, at 2:15, the hour and minute hands form an acute angle.
- The corner of a book: The interior angle of a book's corner is typically acute.
- The angle of a roof's slope: Many house roofs have a slope that creates acute angles with the horizontal.
- The angle of a mountain's peak: The angle formed by two mountain slopes often creates an acute angle.
Properties and Characteristics of Acute Angles
Beyond their definition, acute angles possess several key properties:
- Complementary Angles: Two acute angles are considered complementary if their sum equals 90 degrees. For instance, a 30° angle and a 60° angle are complementary. This property is frequently used in solving geometric problems.
- Sum of Angles in a Triangle: The sum of the three interior angles of any triangle always equals 180 degrees. Therefore, if a triangle contains one right angle, the other two must be acute and complementary. If a triangle has three acute angles, their sum is still 180 degrees.
- Inequalities in Triangles: In any triangle, the longest side is opposite the largest angle. Since acute angles are less than 90 degrees, triangles with acute angles have specific relationships between their sides and angles.
Acute Angles and Triangles: A Deeper Dive
Triangles are classified based on their angles:
- Acute Triangle: A triangle with three acute angles.
- Right Triangle: A triangle with one right angle.
- Obtuse Triangle: A triangle with one obtuse angle.
Understanding the relationship between angles and sides in triangles is essential for solving various geometric problems. The Law of Sines and the Law of Cosines are powerful tools used to determine unknown sides and angles in triangles, including acute triangles.
Applications of Acute Angles: Beyond Geometry
The importance of acute angles extends far beyond the realm of pure geometry. They are fundamental in various fields:
- Engineering: In civil engineering, acute angles are crucial in designing stable structures like bridges and buildings. The angles of support beams and trusses directly impact the structural integrity of the entire construction. Mechanical engineering also utilizes acute angles in designing gears, levers, and other mechanical components.
- Architecture: Architects use acute angles to create aesthetically pleasing and functional designs. Many architectural marvels incorporate acute angles to enhance visual appeal and structural strength.
- Computer Graphics and Animation: The creation of realistic images and animations heavily relies on the accurate representation of angles, including acute angles. Computer graphics algorithms utilize angular calculations to determine object positions, rotations, and perspectives.
- Navigation and Surveying: Acute angles are vital in navigation, particularly when using triangulation methods for determining location. Surveying also depends on accurate angular measurements to create detailed maps and land plots.
- Physics and Optics: In physics, the study of light refraction and reflection frequently involves calculations with acute angles. The angle of incidence and angle of reflection are critical concepts in optics. Similarly, the study of projectile motion involves acute angles to understand the trajectory of launched objects.
Acute Angles in Trigonometry: Sine, Cosine, and Tangent
Trigonometry, the study of triangles, extensively uses acute angles. The fundamental trigonometric functions—sine, cosine, and tangent—are defined in relation to the angles of a right-angled triangle. These functions relate the angles to the ratios of the sides of the triangle, providing a powerful tool for solving problems involving angles and distances.
For an acute angle θ in a right-angled triangle:
- Sine (sin θ) = opposite side / hypotenuse
- Cosine (cos θ) = adjacent side / hypotenuse
- Tangent (tan θ) = opposite side / adjacent side
These functions are critical in many applications, including:
- Calculating distances: Measuring inaccessible distances using angles and known lengths.
- Analyzing forces and vectors: Resolving forces into components.
- Determining heights and angles: Calculating the height of a building or the angle of elevation of an object.
Advanced Concepts Related to Acute Angles
While acute angles are relatively straightforward to understand, they are integral to more complex mathematical ideas:
- Vectors and Scalar Projections: Vectors can be broken down into components using acute angles. The scalar projection of one vector onto another is a key concept involving acute angles.
- Unit Circle: The unit circle in trigonometry uses acute angles to define trigonometric functions for angles beyond 90 degrees.
- Complex Numbers: The argument (angle) of a complex number can be an acute angle.
- Calculus: Derivatives and integrals of trigonometric functions frequently involve acute angles.
Solving Problems Involving Acute Angles
Many problems involve calculating unknown angles or sides in geometric shapes containing acute angles. These problems often require the application of:
- Geometric theorems: Such as the Pythagorean theorem (for right-angled triangles).
- Trigonometric functions: Using sine, cosine, and tangent to solve for unknown angles or sides.
- Algebraic manipulation: Solving equations to find unknown values.
By mastering the concepts related to acute angles and applying the appropriate tools, one can confidently tackle many challenging geometric and trigonometric problems.
Conclusion: The Ubiquity of Acute Angles
Acute angles, though seemingly simple in their definition, are fundamental geometric entities with far-reaching applications. Their importance spans numerous disciplines, highlighting their role as a cornerstone of mathematical understanding and practical applications in various fields. From the design of skyscrapers to the workings of sophisticated computer graphics, acute angles play a vital, often unseen, role in shaping our world. A thorough understanding of acute angles is not merely an academic exercise but a key to comprehending the geometry and trigonometry that underpin our physical reality. The exploration of acute angles is a journey into the fundamental building blocks of mathematics and its numerous applications.
Latest Posts
Latest Posts
-
The Five Carbon Sugar In Rna Is Called
May 11, 2025
-
Which Sentence Uses A Prepositional Phrase
May 11, 2025
-
How To Write A Check For 1250 00
May 11, 2025
-
The Momentum Of An Object Depends Upon The Objects
May 11, 2025
-
What Is The Molar Mass Of S
May 11, 2025
Related Post
Thank you for visiting our website which covers about An Angle With A Measure Less Than 90 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.