All Of The Factors Of 32
Juapaving
Apr 01, 2025 · 5 min read
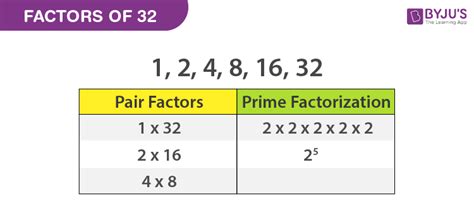
Table of Contents
All the Factors of 32: A Deep Dive into Number Theory
Finding all the factors of a number might seem like a simple task, especially for a relatively small number like 32. However, understanding the process behind identifying factors unlocks a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This article will explore all the factors of 32, delve into the methods for finding factors of any number, and discuss the significance of factors in mathematics.
What are Factors?
Before we dive into the specific factors of 32, let's define what a factor is. A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number.
Finding the Factors of 32
To find all the factors of 32, we can employ a systematic approach. One method involves systematically checking each whole number from 1 up to 32 to see if it divides 32 without leaving a remainder. However, a more efficient method involves considering pairs of factors.
We begin by knowing that 1 and 32 are always factors of any number (except 0). Then, we can look for pairs:
- 2 x 16 = 32
- 4 x 8 = 32
Notice that we've already found all the factor pairs. There are no other whole numbers that multiply to give 32. Therefore, the complete list of factors of 32 is: 1, 2, 4, 8, 16, and 32.
Prime Factorization and its Role in Finding Factors
A powerful tool in number theory for finding all the factors of a number is prime factorization. Prime factorization involves expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 32:
32 can be divided by 2: 32 = 2 x 16
16 can also be divided by 2: 16 = 2 x 8
8 can be divided by 2: 8 = 2 x 4
4 can be divided by 2: 4 = 2 x 2
Therefore, the prime factorization of 32 is 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>.
Knowing the prime factorization is crucial because it allows us to systematically determine all the factors. To find all factors, we consider all possible combinations of the prime factors. In the case of 32 (2<sup>5</sup>):
- 2<sup>0</sup> = 1
- 2<sup>1</sup> = 2
- 2<sup>2</sup> = 4
- 2<sup>3</sup> = 8
- 2<sup>4</sup> = 16
- 2<sup>5</sup> = 32
This method ensures we haven't missed any factors.
Types of Factors: A Deeper Look
Understanding the different types of factors provides further insight into number theory.
-
Proper Factors: These are all factors of a number excluding the number itself. For 32, the proper factors are 1, 2, 4, 8, and 16.
-
Improper Factor: This is simply the number itself. For 32, the improper factor is 32.
-
Prime Factors: As discussed earlier, these are the prime numbers that multiply to give the original number. For 32, the only prime factor is 2.
-
Composite Factors: These are factors that are not prime numbers. For 32, the composite factors are 4, 8, 16, and 32.
The Significance of Factors in Mathematics and Beyond
The concept of factors isn't just an abstract mathematical idea; it has significant practical applications:
-
Cryptography: The security of many encryption algorithms relies heavily on the difficulty of factoring large numbers into their prime factors. This is the basis of RSA encryption, a widely used method for securing online communications.
-
Computer Science: Factorization plays a role in various algorithms used in computer science, such as the greatest common divisor (GCD) algorithm, which finds the largest number that divides two or more integers without leaving a remainder. This has applications in areas such as computer graphics and signal processing.
-
Modular Arithmetic: Understanding factors is crucial in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). This is used in many applications, including cryptography and computer programming.
-
Divisibility Rules: The concept of factors underlies divisibility rules, shortcuts to determine if a number is divisible by another number without performing long division. For example, a number is divisible by 2 if its last digit is even. This stems from the fact that 2 is a factor of even numbers.
-
Algebra: Factorization is a fundamental technique in algebra, used to simplify expressions, solve equations, and analyze functions.
Finding Factors of Larger Numbers: Advanced Techniques
While manually finding factors of small numbers is straightforward, dealing with larger numbers requires more sophisticated techniques. These include:
-
Trial Division: This involves systematically testing all prime numbers up to the square root of the number to check for divisibility. This is more efficient than testing all numbers up to the number itself.
-
Pollard's Rho Algorithm: This is a probabilistic algorithm for integer factorization, particularly useful for factoring large composite numbers.
-
General Number Field Sieve (GNFS): This is the most efficient known algorithm for factoring very large numbers, commonly used in cryptography.
Conclusion: The Importance of Understanding Factors
Understanding factors is fundamental to number theory and has far-reaching consequences in various fields. While finding the factors of 32 might seem trivial, the process reveals a deeper understanding of mathematical concepts that underpin many modern technologies and applications. From simple divisibility rules to complex cryptographic algorithms, the ability to identify and manipulate factors is a key skill in mathematics and computer science. The systematic approaches discussed, including prime factorization, provide efficient methods for tackling this problem, regardless of the number's size. As we’ve seen, even a seemingly simple number like 32 holds a wealth of mathematical significance, showcasing the beauty and power of number theory.
Latest Posts
Latest Posts
-
How Many Miles Are In 10 Kilometers
Apr 02, 2025
-
Where In A Plant Cell Does Photosynthesis Occur
Apr 02, 2025
-
A Motor And A Generator Are
Apr 02, 2025
-
Allows Materials In And Out Of The Cell
Apr 02, 2025
-
Which Of The Following Is Matched Correctly
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about All Of The Factors Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
