A Trapezoid Is A Quadrilateral With Exactly One Pair Of
Juapaving
Mar 24, 2025 · 5 min read
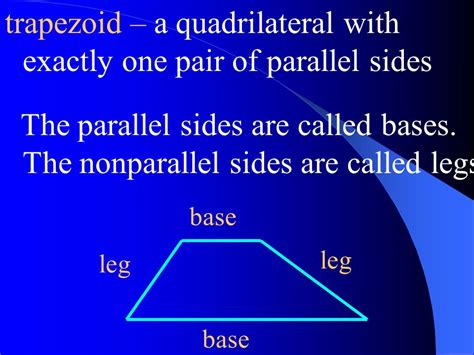
Table of Contents
A Trapezoid is a Quadrilateral with Exactly One Pair of Parallel Sides
A trapezoid, also known as a trapezium in some parts of the world, is a fascinating geometric shape with unique properties. Its defining characteristic? It's a quadrilateral—a four-sided polygon—with exactly one pair of parallel sides. Understanding this fundamental characteristic unlocks a world of mathematical exploration, from calculating its area to exploring its relationship with other quadrilaterals. This comprehensive guide delves deep into the world of trapezoids, exploring their properties, types, formulas, and applications.
Defining Characteristics of a Trapezoid
Let's start with the basics. A trapezoid is a four-sided polygon where at least one pair of opposite sides are parallel. These parallel sides are known as the bases of the trapezoid, often denoted as b₁ and b₂. The non-parallel sides are called the legs or lateral sides.
It's crucial to understand the distinction between a trapezoid and other quadrilaterals. While all trapezoids are quadrilaterals, not all quadrilaterals are trapezoids. For example, a parallelogram (which has two pairs of parallel sides) is a special type of trapezoid, but a rectangle, rhombus, or square are all parallelograms and therefore fall under the broader category of trapezoids. This hierarchical relationship is important for correctly categorizing shapes.
Key Differences from Other Quadrilaterals:
- Parallelogram: A parallelogram has two pairs of parallel sides. Trapezoids only have one.
- Rectangle: A rectangle is a parallelogram with four right angles. It has two pairs of parallel sides, unlike a trapezoid.
- Rhombus: A rhombus is a parallelogram with four equal sides. Again, it has two pairs of parallel sides, distinguishing it from a trapezoid.
- Square: A square is both a rectangle and a rhombus, meaning it has two pairs of parallel sides and four equal sides. It's not a trapezoid in the strictest sense.
Understanding these differences is critical for solving geometric problems and applying the correct formulas.
Types of Trapezoids
While the defining characteristic of a trapezoid is its single pair of parallel sides, further classifications exist based on other properties:
1. Isosceles Trapezoid
An isosceles trapezoid is a special type of trapezoid where the two non-parallel sides (legs) are congruent—meaning they have equal lengths. This congruence leads to several other interesting properties:
- Base angles are congruent: The angles at each base are equal. This means that the angles adjacent to each base are congruent.
- Diagonals are congruent: The lengths of the diagonals are equal.
These additional properties are useful in solving problems involving isosceles trapezoids. They provide more avenues for calculation and proof.
2. Right Trapezoid
A right trapezoid is a trapezoid where at least one leg is perpendicular to both bases. This creates a right angle between a base and a leg. This simplifies area calculations, as you can often divide the trapezoid into a rectangle and a right-angled triangle.
3. Scalene Trapezoid
A scalene trapezoid is the most general type. It has no special properties beyond the defining characteristic of one pair of parallel sides. The legs are of unequal lengths, the base angles are unequal, and the diagonals are unequal.
Calculating the Area of a Trapezoid
The area of a trapezoid is calculated using a straightforward formula:
Area = (1/2) * (b₁ + b₂) * h
Where:
- b₁ and b₂ are the lengths of the two parallel bases.
- h is the height of the trapezoid (the perpendicular distance between the two parallel bases).
This formula works for all types of trapezoids—isosceles, right, and scalene. The key is to accurately measure or calculate the lengths of the bases and the height.
Calculating the Perimeter of a Trapezoid
The perimeter of a trapezoid is simply the sum of the lengths of all four sides:
Perimeter = a + b₁ + b₂ + c
Where:
- a and c are the lengths of the non-parallel sides (legs).
- b₁ and b₂ are the lengths of the parallel sides (bases).
This calculation is straightforward and applies to all types of trapezoids.
Advanced Properties and Theorems
Beyond the basic calculations, several more advanced theorems and properties relate to trapezoids:
Midsegment Theorem
The midsegment of a trapezoid is a line segment that connects the midpoints of the two non-parallel sides. The midsegment theorem states that the length of the midsegment is the average of the lengths of the two bases:
Midsegment = (b₁ + b₂) / 2
This theorem is incredibly useful in solving problems where the lengths of the bases are known or need to be determined.
Area using Coordinates
If the vertices of a trapezoid are given as coordinates in a Cartesian plane, you can use the determinant method or shoelace formula to calculate the area. This involves a more complex calculation utilizing the coordinates of the vertices. This approach is particularly useful in coordinate geometry problems.
Applications of Trapezoids
Trapezoids, despite appearing relatively simple, find application in various fields:
- Architecture: Trapezoidal shapes appear in building designs, roof structures, and window frames. The stability and structural integrity of trapezoidal structures make them suitable for various architectural applications.
- Engineering: Trapezoidal cross-sections are used in beams, channels, and other structural components due to their strength and efficiency.
- Art and Design: Trapezoids, with their distinctive shape, are incorporated into artwork, logos, and graphic designs to create visual interest and unique aesthetic appeal.
- Nature: While not as prevalent as other shapes, approximations of trapezoids can be found in natural formations, such as certain types of rock formations or even aspects of plant growth patterns.
Conclusion
The trapezoid, with its single pair of parallel sides, is a fundamental geometric shape with numerous properties and applications. Understanding its defining characteristics, types, and formulas is crucial for solving various geometric problems and appreciating its importance in diverse fields. From calculating area and perimeter to utilizing advanced theorems and exploring real-world applications, the trapezoid offers a wealth of mathematical exploration and practical relevance. This comprehensive guide provides a solid foundation for anyone looking to deepen their understanding of this fascinating quadrilateral. Further exploration can include investigating more complex problems involving trapezoids inscribed within circles, exploring their relationship to other geometric figures, and delving into the history and development of trapezoid geometry.
Latest Posts
Latest Posts
-
Which Of The Following Is True About Hiv
Mar 28, 2025
-
In Which Situation Is The Distance Traveled Proportional To Time
Mar 28, 2025
-
Which Group Of Nonmetals Is The Most Reactive
Mar 28, 2025
-
99 Rounded To The Nearest Tenth
Mar 28, 2025
-
What Percent Is Equivalent To 3 8
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about A Trapezoid Is A Quadrilateral With Exactly One Pair Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
