A Simple Pendulum With Bob Of Mass M
Juapaving
Apr 03, 2025 · 6 min read
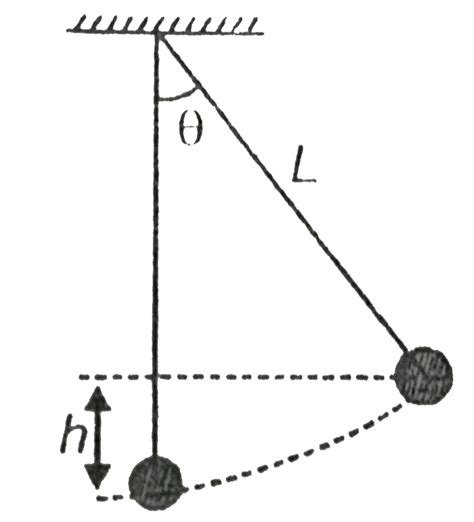
Table of Contents
A Simple Pendulum with a Bob of Mass m: A Deep Dive into Physics
The simple pendulum, a seemingly basic system consisting of a mass (bob) suspended from a fixed point by a massless string or rod, offers a surprisingly rich playground for exploring fundamental concepts in physics. This article delves into the intricacies of a simple pendulum with a bob of mass 'm', examining its motion, derivation of its period, the influence of various factors, and its applications. We'll explore both the idealized model and the realities of real-world pendulums.
Understanding the Idealized Simple Pendulum
The idealized simple pendulum operates under several crucial assumptions:
- Massless String/Rod: The string or rod connecting the bob to the fixed point is considered massless and inextensible (its length remains constant). This simplifies calculations significantly.
- Point Mass: The bob is treated as a point mass, meaning its size and shape are negligible compared to the length of the string. This allows us to focus on the motion of the center of mass.
- No Air Resistance/Friction: The pendulum swings without experiencing air resistance or friction at the pivot point. This eliminates energy loss due to these dissipative forces.
- Small Angle Approximation: For simple harmonic motion (SHM) to apply, the pendulum's swing angle (θ) must be small (typically less than 10 degrees). This allows for the approximation sin θ ≈ θ (where θ is measured in radians).
These assumptions, though simplifying, allow us to derive a mathematically tractable model for understanding the pendulum's behavior.
Deriving the Equation of Motion
Newton's second law, F = ma, forms the basis for deriving the equation of motion. The forces acting on the bob are:
- Gravity: A downward force, mg, where 'g' is the acceleration due to gravity.
- Tension: An upward force, T, exerted by the string.
Resolving the gravitational force into components parallel and perpendicular to the string's direction, we find that the restoring force (the force that pulls the bob back towards its equilibrium position) is proportional to -mg sin θ. Using the small-angle approximation, this simplifies to -mgθ.
Applying Newton's second law along the tangential direction (along the arc of the pendulum's swing), we get:
m * a<sub>t</sub> = -mgθ
where a<sub>t</sub> is the tangential acceleration. Since the arc length, s, is related to the angle θ by s = Lθ (where L is the length of the string), and the tangential acceleration is the second derivative of s with respect to time (d²s/dt²), the equation becomes:
m * L * (d²θ/dt²) = -mgθ
Simplifying, we obtain the second-order differential equation:
(d²θ/dt²) = -(g/L)θ
This is the equation of motion for a simple harmonic oscillator. Its solution is a sinusoidal function, representing the oscillatory motion of the pendulum:
θ(t) = θ<sub>0</sub> cos(ωt + φ)
where:
- θ<sub>0</sub> is the maximum angular displacement (amplitude).
- ω is the angular frequency.
- φ is the phase constant.
Determining the Period and Frequency
From the equation of motion, we can determine the angular frequency:
ω = √(g/L)
The period (T), the time taken for one complete oscillation, is related to the angular frequency by:
T = 2π/ω = 2π√(L/g)
This is the famous formula for the period of a simple pendulum. Notice that the period is independent of the bob's mass (m) – a remarkable result. It depends only on the length of the string (L) and the acceleration due to gravity (g).
Beyond the Idealized Model: Real-World Considerations
The idealized model provides a good approximation for understanding pendulum motion, but real-world pendulums deviate from this ideal due to several factors:
- Air Resistance: Air resistance opposes the pendulum's motion, causing its amplitude to decrease over time (damped oscillation). This damping effect is more significant for larger amplitudes and less dense bobs.
- Friction at the Pivot Point: Friction at the pivot point also dissipates energy, further contributing to damping.
- Finite Mass of the String/Rod: The assumption of a massless string/rod is rarely perfectly true. The mass of the string affects the pendulum's period, especially if the string's mass is comparable to the bob's mass.
- Non-small Angle Oscillations: For larger swing angles, the small-angle approximation (sin θ ≈ θ) breaks down, leading to a period that depends on the amplitude. The period becomes longer than predicted by the simple formula.
- Non-uniform Gravity: The acceleration due to gravity (g) is not perfectly uniform across the Earth's surface. Variations in 'g' affect the period.
Taking these factors into account requires more complex mathematical models that incorporate damping terms, the mass distribution of the pendulum, and a more accurate representation of the gravitational field.
Applications of the Simple Pendulum
The simple pendulum, despite its apparent simplicity, has numerous applications in various fields:
- Measurement of 'g': The pendulum's period can be accurately measured, and using the formula T = 2π√(L/g), the acceleration due to gravity (g) can be determined. This is a classic physics experiment.
- Timekeeping: Historically, the pendulum played a crucial role in the development of accurate clocks and timekeeping devices. The consistent period of the pendulum provided a reliable measure of time.
- Seismometers: Pendulums are used in seismometers to detect and measure ground motion caused by earthquakes. The pendulum's relative inertia resists ground motion, allowing for measurement of seismic waves.
- Educational Demonstrations: The simple pendulum is a valuable tool for demonstrating basic physics principles such as simple harmonic motion, energy conservation, and the effect of gravity.
Advanced Concepts and Extensions
The simple pendulum serves as a springboard to explore more advanced concepts:
- Damped Oscillations: Introducing damping forces (air resistance, friction) leads to damped harmonic motion, where the amplitude decreases exponentially with time.
- Driven Oscillations and Resonance: Applying an external periodic force (driving force) to the pendulum can lead to resonance, where the amplitude of oscillation becomes very large when the driving frequency matches the pendulum's natural frequency.
- Chaotic Pendulums: Under certain conditions (e.g., driven pendulum with large amplitudes), the pendulum's motion can become chaotic, exhibiting unpredictable and sensitive dependence on initial conditions.
- Double Pendulum: A double pendulum, consisting of two pendulums connected in series, exhibits significantly more complex and chaotic motion compared to a simple pendulum.
Conclusion
The simple pendulum, although a seemingly simple system, provides a rich and fascinating area of study. Understanding its behavior, from the idealized model to the complexities of real-world scenarios, allows for a deeper appreciation of fundamental physics principles and their applications. Its enduring importance in physics education and its historical contributions to technology solidify its place as a cornerstone of classical mechanics. Whether exploring its basic properties or delving into its more advanced aspects, the simple pendulum offers endless opportunities for investigation and discovery. The simple formula, T = 2π√(L/g), while a starting point, hides a multitude of intriguing physical phenomena waiting to be unravelled. Further exploration of these topics, including the impact of different damping mechanisms or the transition into chaotic motion, will lead to a greater comprehension of the elegance and depth concealed within this seemingly straightforward physical system. The continuing research and application of the simple pendulum's principles underscores its enduring relevance in various scientific fields.
Latest Posts
Latest Posts
-
Like The Odds Of An Unlikely Event
Apr 04, 2025
-
How Many Grams In 200 Mg
Apr 04, 2025
-
A Movement Along The Demand Curve Is
Apr 04, 2025
-
57 Inches Is How Many Feet
Apr 04, 2025
-
Common Factors Of 12 And 36
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about A Simple Pendulum With Bob Of Mass M . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
