A Rhombus With A Line Of Symmetry
Juapaving
Mar 28, 2025 · 6 min read
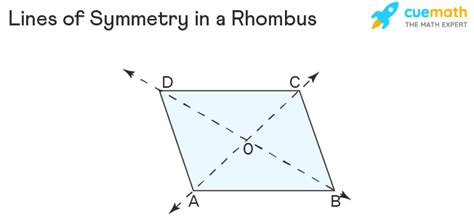
Table of Contents
- A Rhombus With A Line Of Symmetry
- Table of Contents
- A Rhombus with a Line of Symmetry: Exploring Geometric Properties
- Understanding the Rhombus: A Foundation
- Lines of Symmetry in a Rhombus: A Deeper Dive
- Rhombus with Two Lines of Symmetry: Detailed Analysis
- Distinguishing Rhombuses Based on Symmetry
- Applications and Real-World Examples
- Advanced Considerations: Rotational Symmetry and Tessellations
- Conclusion: A Comprehensive Look at Symmetrical Rhombuses
- Latest Posts
- Latest Posts
- Related Post
A Rhombus with a Line of Symmetry: Exploring Geometric Properties
A rhombus, a captivating quadrilateral with all sides equal in length, presents a fascinating case study in geometry, especially when considering its lines of symmetry. While often overlooked, the presence (or absence) of lines of symmetry significantly impacts a rhombus's properties and classifications. This exploration delves deep into the characteristics of a rhombus possessing a line of symmetry, dissecting its geometric intricacies and highlighting its unique features.
Understanding the Rhombus: A Foundation
Before diving into the specifics of a rhombus with a line of symmetry, let's establish a strong foundation by understanding the fundamental properties of a rhombus itself.
A rhombus is defined by four equal sides. This fundamental property immediately sets it apart from other quadrilaterals like squares, rectangles, and parallelograms, though it shares some commonalities. All rhombuses are parallelograms, meaning opposite sides are parallel and equal in length. This parallel property ensures that opposite angles are also equal. However, a rhombus doesn't necessitate right angles like a square.
Key Properties of a Rhombus:
- Four equal sides: This is the defining characteristic of a rhombus.
- Opposite sides are parallel: This property stems from its classification as a parallelogram.
- Opposite angles are equal: A direct consequence of the parallel sides.
- Consecutive angles are supplementary: The sum of any two adjacent angles equals 180 degrees.
- Diagonals bisect each other: The diagonals intersect at a point that divides each diagonal into two equal segments.
- Diagonals bisect the angles: Each diagonal divides a pair of opposite angles into two equal angles.
Lines of Symmetry in a Rhombus: A Deeper Dive
Now, let's focus on the lines of symmetry. A line of symmetry, also known as a reflectional symmetry, divides a shape into two identical halves that are mirror images of each other. Not all rhombuses have lines of symmetry. The existence of these lines depends critically on the angles within the rhombus.
A rhombus can have zero, two, or four lines of symmetry.
-
Zero Lines of Symmetry: A rhombus with no right angles and unequal adjacent angles possesses no lines of symmetry. This represents a general rhombus where the reflection across any potential line doesn't result in a perfect overlap.
-
Two Lines of Symmetry: A rhombus with unequal adjacent angles, but with at least one pair of opposite angles being equal (as is inherent in any rhombus), will have two lines of symmetry. These lines of symmetry are along the diagonals that connect opposite vertices. These diagonals are perpendicular bisectors of each other. Reflecting the rhombus across either of these diagonals produces a congruent shape perfectly overlapping the original.
-
Four Lines of Symmetry: A rhombus with four lines of symmetry is a special case – it's a square. Each diagonal and each line connecting the midpoints of opposite sides forms a line of symmetry. In this instance, all angles are right angles (90 degrees), and the diagonals are equal in length.
Rhombus with Two Lines of Symmetry: Detailed Analysis
Let's focus our attention on the rhombus with two lines of symmetry, as this is the most common scenario beyond the special case of a square.
In a rhombus with two lines of symmetry, those lines of symmetry precisely align with its diagonals. This configuration necessitates some important geometric relationships:
-
Perpendicular Diagonals: The two diagonals are always perpendicular to each other in a rhombus with two lines of symmetry. This perpendicularity is a direct consequence of the reflectional symmetry.
-
Angle Bisectors: Each diagonal acts as an angle bisector, dividing the angles at its endpoints into two equal halves. This again stems from the mirror symmetry across the diagonals.
-
Area Calculation: The area of a rhombus with two lines of symmetry can be easily calculated using the formula: Area = (1/2) * d1 * d2, where d1 and d2 are the lengths of the two diagonals. This simplified formula arises from the fact that the diagonals divide the rhombus into four congruent right-angled triangles.
-
Construction: Constructing a rhombus with two lines of symmetry involves establishing the perpendicularity of its diagonals. Starting with two perpendicular line segments of varying lengths (the diagonals), we can then construct the rhombus by drawing equal-length sides connecting the endpoints of the diagonals.
Distinguishing Rhombuses Based on Symmetry
Understanding the relationship between a rhombus's angles and its lines of symmetry allows us to classify rhombuses effectively.
| Type of Rhombus | Angle Properties | Lines of Symmetry | Diagonals |
|---|---|---|---|
| General Rhombus | No right angles, adjacent angles unequal | 0 | Not necessarily perpendicular |
| Rhombus with Two Lines | No right angles, opposite angles equal | 2 | Perpendicular, angle bisectors |
| Square (Special Rhombus) | All angles are 90 degrees | 4 | Perpendicular, equal in length |
Applications and Real-World Examples
The geometric properties of a rhombus with a line of symmetry are not merely abstract concepts; they find practical applications in various fields:
-
Engineering and Design: The symmetrical properties are utilized in structural design, ensuring stability and balance. Think of the diamond shape used in certain bridge designs or the pattern found in certain tessellations.
-
Crystallography: The rhombus shape appears in certain crystal structures. Understanding its symmetry helps predict the behavior of light and other properties within these structures.
-
Art and Architecture: The visually appealing symmetrical nature of the rhombus is frequently used in art and architectural patterns. Many designs incorporate the rhombus to create aesthetically pleasing arrangements.
-
Computer Graphics: The precise mathematical properties are crucial in computer graphics for generating and manipulating symmetrical shapes. Many programming algorithms rely on understanding the geometrical principles behind this shape.
Advanced Considerations: Rotational Symmetry and Tessellations
Beyond reflectional symmetry, rhombuses can also exhibit rotational symmetry. A square, the special case of a rhombus with four lines of symmetry, possesses rotational symmetry of order 4, meaning it can be rotated by 90, 180, and 270 degrees and still look identical. Other rhombuses may have rotational symmetry of order 2, meaning a 180-degree rotation results in an identical shape.
Moreover, rhombuses, particularly those with specific angle measurements, can be used to create tessellations. Tessellations are patterns made by repeating shapes without gaps or overlaps. Certain rhombuses, due to their symmetrical properties, can create visually appealing and mathematically consistent tessellations, often found in floor tiles, fabric designs, and other art forms.
Conclusion: A Comprehensive Look at Symmetrical Rhombuses
This detailed exploration of a rhombus with a line of symmetry showcases the rich interplay of geometry and symmetry. Understanding the various properties, classifications, and applications of this shape highlights its importance in various aspects of mathematics, design, and real-world scenarios. From the simple definition of equal sides to the nuanced understanding of its lines of symmetry, the rhombus remains a fascinating and versatile geometrical form. The ability to distinguish between different types of rhombuses based on their symmetry provides a deeper understanding of the relationships between geometry and visual properties. This knowledge empowers further exploration of more complex geometrical concepts and their tangible applications.
Latest Posts
Latest Posts
-
How Can The Strength Of An Electromagnet Be Increased
Apr 02, 2025
-
If Qt Is Perpendicular To Pr
Apr 02, 2025
-
Which Base Is Not Present In Rna
Apr 02, 2025
-
What Is The Lcm Of 5 And 10
Apr 02, 2025
-
Air Moves From High To Low Pressure
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A Rhombus With A Line Of Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
