A Circle Has A Circumference Of Units.
Juapaving
Apr 05, 2025 · 5 min read
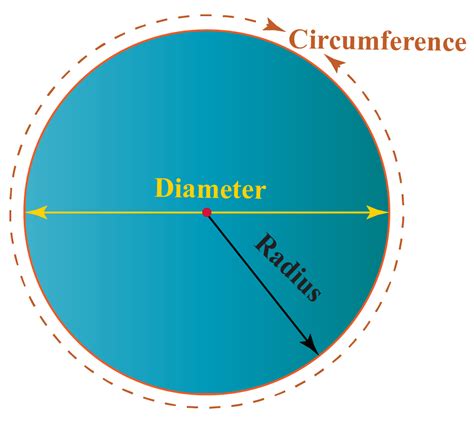
Table of Contents
A Circle Has a Circumference of 'x' Units: Exploring the Properties and Applications
The seemingly simple statement, "a circle has a circumference of 'x' units," opens a door to a rich tapestry of mathematical concepts and real-world applications. Understanding the implications of a circle's circumference, regardless of the specific value of 'x', is fundamental to geometry, trigonometry, and various scientific and engineering disciplines. This article delves deep into the properties and applications associated with a circle's circumference, exploring its relationship with other crucial parameters like radius, diameter, and area, along with practical examples of its use.
Understanding Circumference: Definition and Formula
The circumference of a circle is the linear distance around its edge. It's essentially the perimeter of the circle. The formula for calculating the circumference (C) is directly related to the circle's radius (r) or diameter (d):
- C = 2πr (using the radius)
- C = πd (using the diameter)
Where:
- C represents the circumference
- r represents the radius (the distance from the center of the circle to any point on the circle)
- d represents the diameter (the distance across the circle through its center; d = 2r)
- π (pi) represents the mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter.
The Significance of Pi (π)
Pi is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. This seemingly infinite nature of pi makes it a fascinating and significant mathematical constant. Its presence in the circumference formula highlights the inherent relationship between a circle's diameter and its circumference. Understanding pi is crucial for accurate circumference calculations.
Calculating Circumference: Examples and Applications
Let's explore some examples illustrating circumference calculations and their real-world applications:
Example 1: Finding the Circumference Given the Radius
A circular garden has a radius of 5 meters. What is its circumference?
Using the formula C = 2πr, we substitute r = 5 meters:
C = 2 * π * 5 meters ≈ 31.42 meters
Therefore, the garden's circumference is approximately 31.42 meters.
Example 2: Finding the Circumference Given the Diameter
A circular track has a diameter of 100 yards. What is its circumference?
Using the formula C = πd, we substitute d = 100 yards:
C = π * 100 yards ≈ 314.16 yards
Therefore, the track's circumference is approximately 314.16 yards.
Example 3: Real-World Application: Designing a Circular Pool
An architect is designing a circular swimming pool. The pool's circumference needs to be 75 feet to accommodate a specific number of swimmers. What should the radius of the pool be?
We can rearrange the formula C = 2πr to solve for r:
r = C / (2π)
Substituting C = 75 feet:
r = 75 feet / (2π) ≈ 11.94 feet
The architect should design the pool with a radius of approximately 11.94 feet.
Beyond Circumference: Relationship with Other Circular Properties
The circumference is intrinsically linked to other important properties of a circle:
Relationship with Radius and Diameter
As already shown, the circumference is directly proportional to both the radius and the diameter. Doubling the radius or diameter will double the circumference. This linear relationship is crucial for understanding scaling and proportions in circular objects.
Relationship with Area
The area (A) of a circle is given by the formula: A = πr²
While not directly proportional, the circumference and area are related through the radius. Knowing the circumference allows us to calculate the radius (r = C / 2π) and subsequently calculate the area. This is particularly useful in applications involving both the perimeter and the enclosed space of a circle.
Advanced Applications of Circumference
The concept of circumference extends beyond basic geometry and finds application in numerous fields:
Engineering and Design
- Wheel Design: Circumference is crucial in calculating the distance traveled by a wheel in one revolution. This is fundamental in designing vehicles, machinery, and various mechanical systems.
- Piping and Cable Lengths: In engineering projects, calculating the length of pipes, cables, or belts that wrap around circular components necessitates accurate circumference calculations.
- Circular Structures: The circumference is essential in designing and constructing circular structures such as stadiums, water tanks, and other cylindrical or spherical objects.
Science and Physics
- Orbital Mechanics: In astronomy, the circumference of a planet's orbit is vital in calculating orbital periods and velocities.
- Circular Motion: In physics, the concept of angular velocity and acceleration in circular motion is directly tied to the circumference.
- Wave Phenomena: The circumference is relevant in understanding wave propagation in circular patterns, such as ripples in water or sound waves emanating from a point source.
Everyday Applications
- Calculating the Length of a Track: Athletes often use the circumference of a running track to plan training regimens.
- Baking and Cooking: The circumference is useful when calculating the amount of dough needed for a circular pie crust or pizza base.
- Gardening and Landscaping: Gardeners need to consider the circumference when planning fences or pathways around circular gardens.
Solving Problems Involving Circumference: A Step-by-Step Approach
Solving problems involving circumference often requires a systematic approach:
- Identify the known variables: Determine if the radius, diameter, or circumference is given.
- Choose the appropriate formula: Use the formula C = 2πr or C = πd based on the given information.
- Substitute the known values: Plug the known values into the formula.
- Solve for the unknown variable: Perform the calculations to find the desired value (circumference, radius, or diameter).
- Check your answer: Ensure your answer is reasonable and consistent with the given information.
Conclusion: The Ubiquitous Circle and its Circumference
The seemingly simple concept of a circle's circumference underlies a vast array of mathematical principles and practical applications. From the fundamental relationship with pi to its crucial role in engineering, science, and everyday life, understanding the calculation and significance of circumference is essential for anyone seeking a deeper appreciation of mathematics and its impact on the world around us. The next time you encounter a circle, remember the power and versatility hidden within its seemingly simple circumference. Mastering the calculation and understanding its implications will unlock a deeper understanding of geometry and its boundless applications.
Latest Posts
Latest Posts
-
Venn Diagram Cellular Respiration And Photosynthesis
Apr 06, 2025
-
What Joint Do You Use To Lift The Weight
Apr 06, 2025
-
Balanced Chemical Equation For Neutralization Of Acid With Naoh
Apr 06, 2025
-
Why Is Ice Melting Not A Chemical Reaction
Apr 06, 2025
-
The Lcm Of 6 And 10
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about A Circle Has A Circumference Of Units. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
