9.8 M S2 To Ft S2
Juapaving
May 24, 2025 · 5 min read
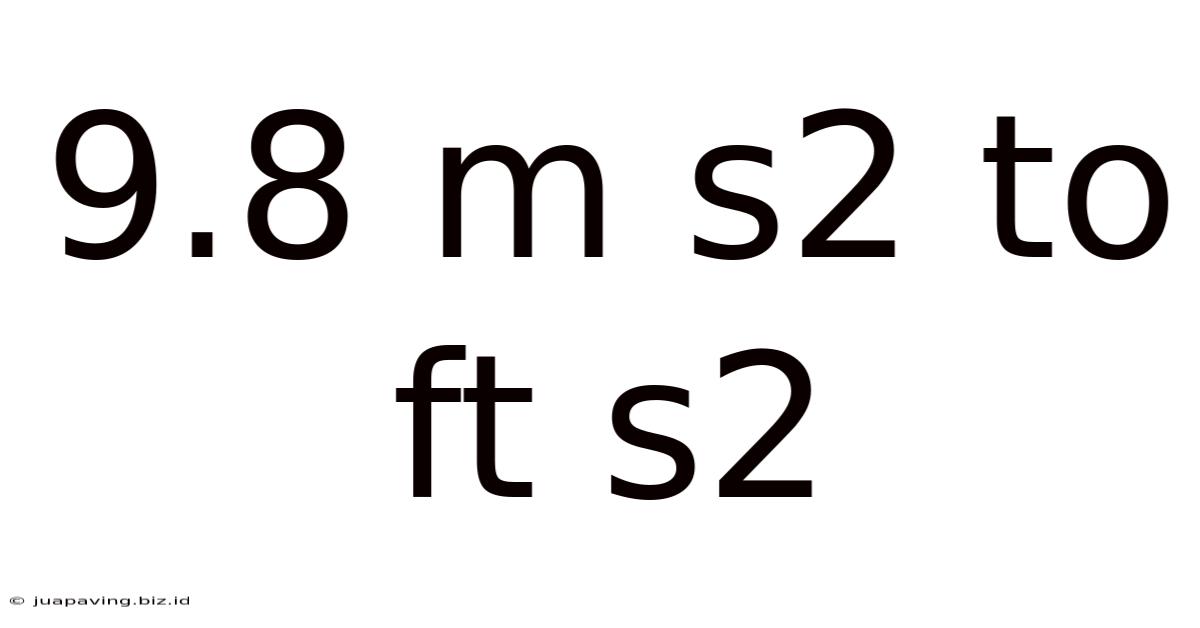
Table of Contents
9.8 m/s² to ft/s²: A Comprehensive Guide to Unit Conversion and its Significance in Physics
The seemingly simple conversion of 9.8 m/s² (meters per second squared), the standard acceleration due to gravity on Earth, to ft/s² (feet per second squared) might seem trivial at first glance. However, understanding this conversion delves into the fundamental principles of unit systems, dimensional analysis, and the practical implications of using different units in physics and engineering. This article will provide a detailed explanation of this conversion, exploring its methods, significance, and applications.
Understanding Units and Unit Systems
Before diving into the conversion, let's establish a firm understanding of units and unit systems. Units are standardized quantities used to measure physical quantities. Different unit systems exist, with the most common being the International System of Units (SI) and the Imperial system (or US customary units).
-
SI System: This is the globally accepted system, employing meters (m), kilograms (kg), and seconds (s) as fundamental units for length, mass, and time, respectively. Acceleration, being the rate of change of velocity, is expressed in m/s².
-
Imperial System: This system, predominantly used in the United States, utilizes feet (ft), pounds (lb), and seconds (s) as its fundamental units. Acceleration in this system is expressed in ft/s².
The difference between these systems lies in the definitions of their base units. This necessitates conversion factors when working across different systems.
The Conversion: 9.8 m/s² to ft/s²
The conversion from meters to feet is crucial for this calculation. The established conversion factor is:
1 meter (m) ≈ 3.28084 feet (ft)
This means that one meter is approximately equal to 3.28084 feet. To convert 9.8 m/s² to ft/s², we simply multiply the value by the conversion factor:
9.8 m/s² * 3.28084 ft/m ≈ 32.15 ft/s²
Therefore, 9.8 m/s² is approximately equal to 32.15 ft/s². It's crucial to note that this is an approximation due to the approximate nature of the conversion factor. More precise conversions may utilize more decimal places in the conversion factor, depending on the required accuracy.
Step-by-Step Calculation:
- Identify the conversion factor: 1 m ≈ 3.28084 ft
- Set up the conversion: 9.8 m/s² * (3.28084 ft/1 m)
- Cancel out units: The 'm' units cancel out, leaving ft/s².
- Perform the multiplication: 9.8 * 3.28084 ≈ 32.152472 ft/s²
- Round to appropriate significant figures: Given that 9.8 has two significant figures, we round the result to 32 ft/s².
Significance of the Conversion
The conversion of 9.8 m/s² to ft/s² holds significant importance in several contexts:
-
Cross-System Compatibility: Many engineering projects involve collaboration between teams using different unit systems. Converting between SI and Imperial units ensures consistent data interpretation and avoids errors.
-
Historical Context: While the SI system is dominant today, many older engineering documents and designs utilize the Imperial system. Converting to the appropriate unit system is essential for understanding and working with these documents.
-
Educational Purposes: Understanding unit conversions reinforces fundamental concepts of dimensional analysis and the relationship between different unit systems. It is a crucial aspect of physics and engineering education.
-
Calculations involving gravity: The value of gravitational acceleration (9.8 m/s² or 32.15 ft/s²) is frequently used in physics calculations related to projectile motion, free fall, and other gravitational phenomena. Using the appropriate unit system is crucial for obtaining correct results in these calculations.
Applications in Physics and Engineering
The conversion of gravitational acceleration finds applications in various areas:
-
Projectile Motion: Calculations involving projectile trajectories and range require accurate values of gravitational acceleration in the chosen unit system.
-
Orbital Mechanics: While the gravitational constant (G) is usually expressed in SI units, understanding the acceleration due to gravity in different systems is crucial for various calculations in satellite dynamics and orbital mechanics.
-
Fluid Mechanics: Calculations involving buoyancy, pressure, and other fluid properties might require using the appropriate unit system for consistency.
-
Structural Engineering: The value of gravitational acceleration is used to calculate stresses and strains in structures, especially in situations involving dead loads (weights of building materials).
-
Mechanical Engineering: Calculations involving forces, acceleration, and motion often require consistent unit systems to obtain correct results.
Beyond the Basic Conversion: Dimensional Analysis
The conversion process highlighted above is a simple form of dimensional analysis. Dimensional analysis is a powerful tool for checking the consistency of equations and units in physical problems. It involves ensuring that the units on both sides of an equation match. This serves as a valuable error-checking mechanism in complex calculations.
For example, in the equation F = ma (Force = mass x acceleration), the units must be consistent:
- In SI units: Newtons (N) = kilograms (kg) * meters/second² (m/s²)
- In Imperial units: Pounds (lb) = slugs (lb⋅s²/ft) * feet/second² (ft/s²)
Dimensional analysis helps identify inconsistencies and errors in equations before numerical calculations are performed.
Advanced Considerations and Potential Pitfalls
While the conversion itself is straightforward, several subtle points warrant attention:
-
Approximation: The conversion factor (3.28084) is an approximation. Higher precision might be necessary for extremely accurate calculations. Using a more precise conversion factor can improve the accuracy of the result.
-
Contextual Relevance: The choice between using m/s² or ft/s² often depends on the context of the problem. Following established conventions within a specific field or discipline is crucial.
-
Unit consistency: Maintain unit consistency throughout the entire calculation to avoid errors. Mixing units from different systems can lead to incorrect results.
-
Significant figures: Pay close attention to the number of significant figures in both the initial value and the conversion factor to ensure that the final answer reflects the appropriate level of precision.
Conclusion
The seemingly simple conversion of 9.8 m/s² to ft/s² illustrates the fundamental importance of understanding unit systems and dimensional analysis in physics and engineering. While the numerical conversion is straightforward, its implications extend far beyond a simple mathematical operation. The ability to seamlessly convert between units is essential for effective problem-solving, collaboration, and accurate interpretation of results across diverse applications. By mastering this fundamental concept, practitioners in various scientific and engineering fields can confidently tackle complex problems involving acceleration and other physical quantities. The understanding gained from this conversion forms the bedrock for tackling more advanced problems in various fields.
Latest Posts
Latest Posts
-
Each Individual Outcome Of An Experiment Is Called
May 24, 2025
-
To Kill A Mockingbird Chapter 29 Summary
May 24, 2025
-
Match Each Definition With The Correct Term
May 24, 2025
-
Pogil Electron Energy And Light Answers
May 24, 2025
-
9 3 4 Packet Tracer Data Center Exploration
May 24, 2025
Related Post
Thank you for visiting our website which covers about 9.8 M S2 To Ft S2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.