8 Is What Percent Of 5
Juapaving
May 14, 2025 · 4 min read
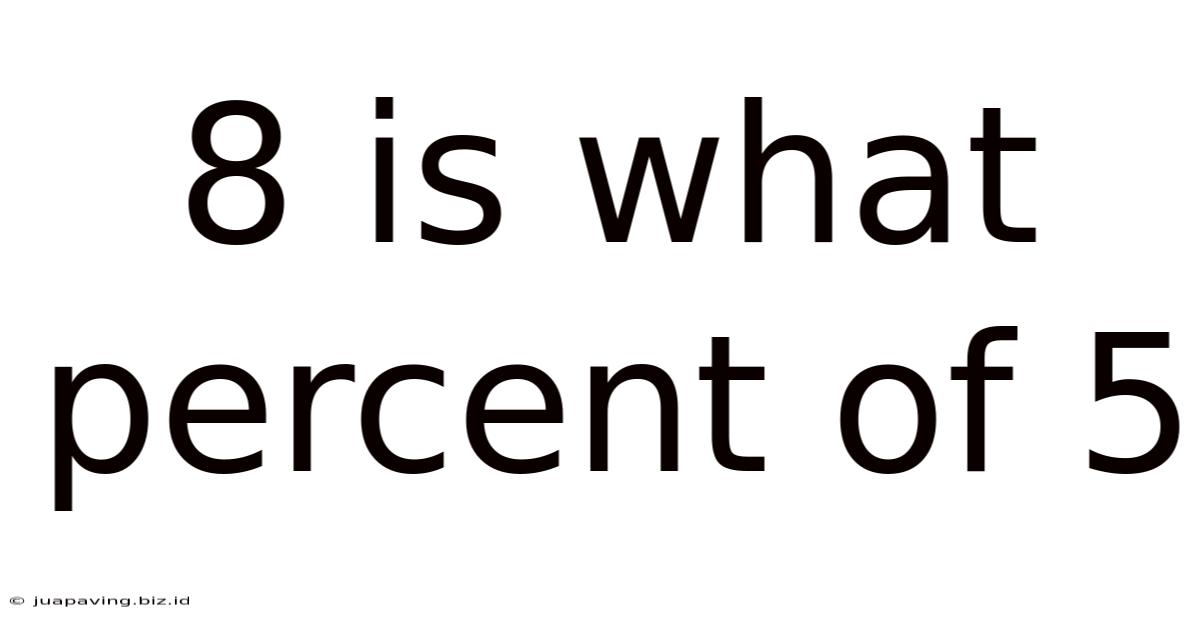
Table of Contents
8 is What Percent of 5? Understanding Percentages and Proportions
This seemingly simple question, "8 is what percent of 5?", delves into the fundamental concepts of percentages and proportions. While the answer might seem counterintuitive at first glance (because 8 is larger than 5), understanding the underlying mathematical principles is crucial for a wide range of applications, from everyday budgeting and shopping to complex scientific calculations and financial analysis. This article will not only provide the solution but also explore the various methods to solve this type of problem and delve into the broader significance of percentages and proportions.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 1% represents 1/100, 50% represents 50/100 (or 1/2), and 100% represents 100/100 (or the whole). Percentages provide a standardized and easily understandable way to compare and represent proportions.
Solving "8 is What Percent of 5?"
The question "8 is what percent of 5?" can be translated into a mathematical equation. Let's represent the unknown percentage as 'x'. We can write the equation as:
8 = x% * 5
To solve for 'x', we need to isolate it on one side of the equation. Here are two common methods:
Method 1: Using the Equation Directly
-
Rewrite the percentage: We convert x% to its decimal equivalent by dividing by 100: x% = x/100
-
Substitute and solve: The equation becomes: 8 = (x/100) * 5
-
Multiply both sides by 100: 800 = 5x
-
Divide both sides by 5: x = 800/5 = 160
Therefore, 8 is 160% of 5.
Method 2: Using Proportions
This method involves setting up a proportion, which equates two ratios.
-
Set up the proportion: We can represent the problem as a ratio: 8/5 = x/100
-
Cross-multiply: This gives us 8 * 100 = 5 * x
-
Solve for x: 800 = 5x => x = 800/5 = 160
Again, we find that x = 160. Therefore, 8 is 160% of 5.
Why is the Percentage Greater Than 100%?
The result of 160% might seem surprising at first because 8 is larger than 5. However, it's perfectly valid to have a percentage greater than 100%. This simply means that the first number (8) is more than the whole of the second number (5). It represents a value that exceeds the reference value (5).
Real-World Applications of Percentages and Proportions
Understanding percentages and proportions is fundamental in many real-world scenarios:
1. Finance:
- Interest calculations: Calculating simple and compound interest relies heavily on percentages.
- Investment returns: Expressing investment gains or losses as percentages allows for easy comparison across different investments.
- Budgeting: Percentages are essential for budgeting, tracking expenses, and allocating resources effectively. For instance, determining what percentage of your income is allocated to rent, food, or entertainment.
- Loan repayments: Understanding loan interest rates and calculating monthly repayments involves working with percentages.
2. Business:
- Profit margins: Calculating profit margins (profit as a percentage of revenue) is crucial for business profitability analysis.
- Sales growth: Expressing sales growth as a percentage allows for easy tracking and comparison over time.
- Market share: Market share is often expressed as a percentage of the total market.
- Discount calculations: Determining discounts in sales or promotions requires calculating percentages.
3. Science:
- Statistical analysis: Percentages are used extensively in statistical analysis to represent proportions and probabilities.
- Scientific measurements: Expressing experimental results as percentages is common in scientific reports. For example, the percentage of successful trials in an experiment.
4. Everyday Life:
- Shopping: Calculating discounts, sales tax, or tips involves using percentages.
- Cooking: Adjusting recipes based on the number of servings frequently involves working with proportions.
- Health and fitness: Tracking progress in fitness goals, such as weight loss or muscle gain, often involves calculating percentages of change.
Expanding the Understanding: Variations and Extensions
The core concept illustrated by the question "8 is what percent of 5?" can be extended to more complex problems. For example:
- Finding the base: "8 is 160% of what number?" This requires rearranging the equation to solve for the base (the number 5 in our original example).
- Finding the percentage change: Calculating percentage increase or decrease involves comparing two values and expressing the difference as a percentage of the original value. This is crucial for analyzing trends and changes over time in various fields.
- Compound percentages: Situations that involve successive percentage changes require a more nuanced approach, typically involving repeated multiplications rather than simple addition.
Conclusion
The seemingly simple question, "8 is what percent of 5?", provides a gateway to understanding the powerful concepts of percentages and proportions. Mastering these concepts equips individuals with essential skills applicable across various domains, from personal finance to complex scientific calculations. By understanding the underlying mathematical principles and various methods of solving such problems, one can confidently tackle real-world challenges and gain a deeper understanding of quantitative data. The ability to convert between fractions, decimals, and percentages is a fundamental skill for numeracy and problem-solving in virtually any field. The answer to the question—160%—is not just a numerical solution but a representation of a proportional relationship, highlighting that percentages can exceed 100% when comparing a larger value to a smaller reference value.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.