75 Is What Percent Of 250
Juapaving
May 11, 2025 · 5 min read
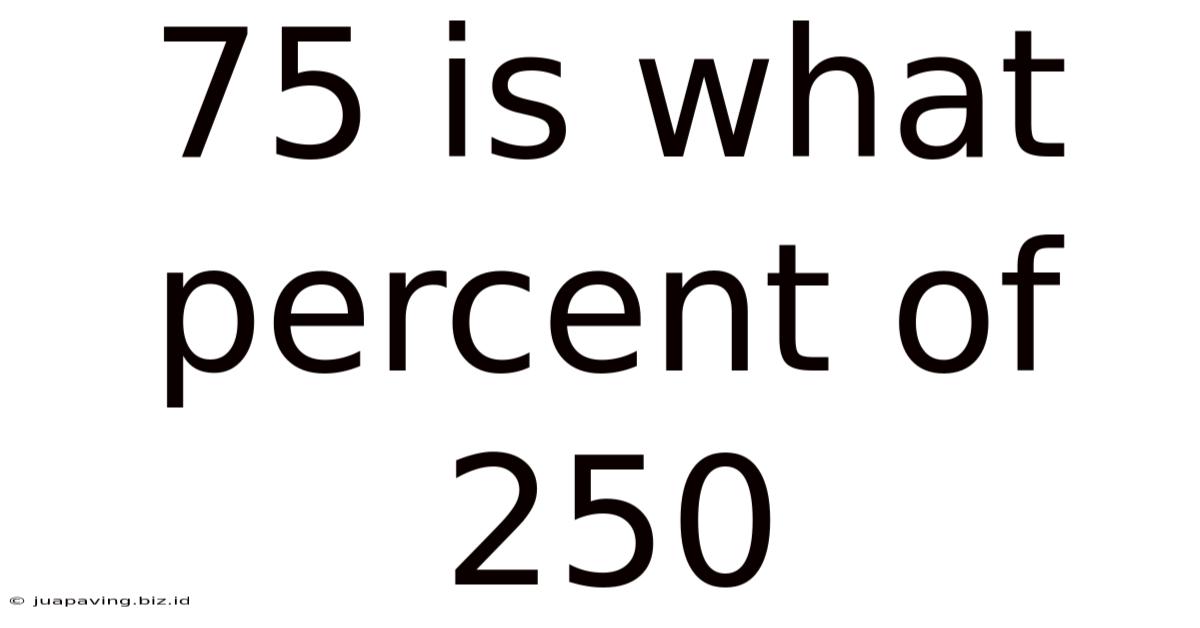
Table of Contents
75 is What Percent of 250: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into the question, "75 is what percent of 250?", providing a step-by-step solution, exploring various methods, and expanding on the broader concept of percentage calculations. We'll also look at practical applications and common mistakes to avoid.
Understanding the Fundamentals of Percentages
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2 (one-half).
Key Terms and Concepts
- Percentage: The ratio expressed as a number out of 100.
- Base: The total amount or the whole quantity. In our problem, 250 is the base.
- Part: The portion of the base that we are interested in. In our problem, 75 is the part.
- Rate: The percentage that the part represents of the base. This is what we are trying to find.
Calculating "75 is What Percent of 250?" - Method 1: The Formula Approach
The most straightforward method involves using the percentage formula:
(Part / Base) x 100 = Percentage
Let's substitute the values from our problem:
(75 / 250) x 100 = Percentage
- Divide the part by the base: 75 / 250 = 0.3
- Multiply the result by 100: 0.3 x 100 = 30
Therefore, 75 is 30% of 250.
Calculating "75 is What Percent of 250?" - Method 2: Proportion Method
The proportion method provides an alternative approach, particularly useful for visualizing the relationship between the parts and the whole. We set up a proportion:
75 / 250 = x / 100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
75 * 100 = 250 * x
7500 = 250x
Now, divide both sides by 250:
x = 7500 / 250
x = 30
Again, we find that 75 is 30% of 250.
Applying Percentage Calculations in Real-World Scenarios
Understanding percentage calculations is crucial for navigating everyday situations. Here are a few examples:
1. Sales and Discounts:
Imagine a store offering a 30% discount on an item originally priced at $250. To calculate the discount amount, you'd use the same principle:
30% of $250 = (30/100) * $250 = $75
The discounted price would be $250 - $75 = $175
2. Tax Calculations:
If a sales tax is 6%, and you purchase an item for $250, the tax amount would be:
6% of $250 = (6/100) * $250 = $15
The total cost, including tax, would be $250 + $15 = $265.
3. Grade Calculations:
Suppose you scored 75 points out of a possible 250 points on a test. Your percentage score would be:
(75 / 250) * 100 = 30%
4. Financial Analysis:
Percentage calculations are fundamental in finance, used to track growth, analyze profits and losses, and calculate interest rates.
Common Mistakes to Avoid When Calculating Percentages
Several common errors can lead to inaccurate results. Let's address some of them:
1. Incorrect Order of Operations:
Always follow the order of operations (PEMDAS/BODMAS). Ensure you divide before multiplying by 100.
2. Confusing Part and Base:
Clearly identify the part (the portion) and the base (the whole) before applying the formula. Mistaking one for the other will lead to an incorrect percentage.
3. Incorrect Decimal Placement:
When multiplying by 100, ensure you move the decimal point two places to the right. A misplaced decimal will result in an incorrect answer.
4. Using Incorrect Formulae:
Ensure you are using the appropriate formula for the type of percentage calculation you are performing. There are different formulas for calculating percentage increase, percentage decrease, and percentage change.
Expanding on Percentage Concepts: Percentage Increase and Decrease
While the problem "75 is what percent of 250?" focuses on determining a percentage of a whole, let's explore related concepts:
Percentage Increase: This refers to the increase in a value expressed as a percentage of the original value. For instance, if a value increases from 200 to 250, the percentage increase is calculated as follows:
- Find the difference: 250 - 200 = 50
- Divide the difference by the original value: 50 / 200 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
Therefore, there is a 25% increase from 200 to 250.
Percentage Decrease: This is the decrease in a value expressed as a percentage of the original value. If a value decreases from 250 to 200, the percentage decrease is:
- Find the difference: 250 - 200 = 50
- Divide the difference by the original value: 50 / 250 = 0.2
- Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Therefore, there is a 20% decrease from 250 to 200.
Advanced Percentage Applications and Problem Solving
Percentage calculations are integral to many advanced mathematical and statistical concepts:
- Compound Interest: Calculating interest earned on both the principal amount and accumulated interest.
- Statistical Analysis: Determining percentages within data sets for creating graphs, charts and interpreting trends.
- Financial Modeling: Building financial models to predict future performance based on percentage changes.
Mastering percentage calculations is a valuable skill that extends far beyond basic arithmetic. It’s a cornerstone for understanding and applying mathematical concepts in various real-world scenarios. By understanding the fundamentals, utilizing appropriate formulas, and avoiding common errors, you can confidently tackle any percentage-related problem. Remember to always clearly define the part, base, and the goal of your calculation for accurate and efficient problem-solving.
Latest Posts
Latest Posts
-
What Does Alcl3 Do In A Reaction
May 13, 2025
-
How Are Factors And Multiples Related
May 13, 2025
-
Money Needed To Start A Business Is Called
May 13, 2025
-
What Are The End Products Of Starch Digestion
May 13, 2025
-
What Are Polymers Of Amino Acids
May 13, 2025
Related Post
Thank you for visiting our website which covers about 75 Is What Percent Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.