7 Is Subtracted From The Square Of A Number.
Juapaving
May 12, 2025 · 5 min read
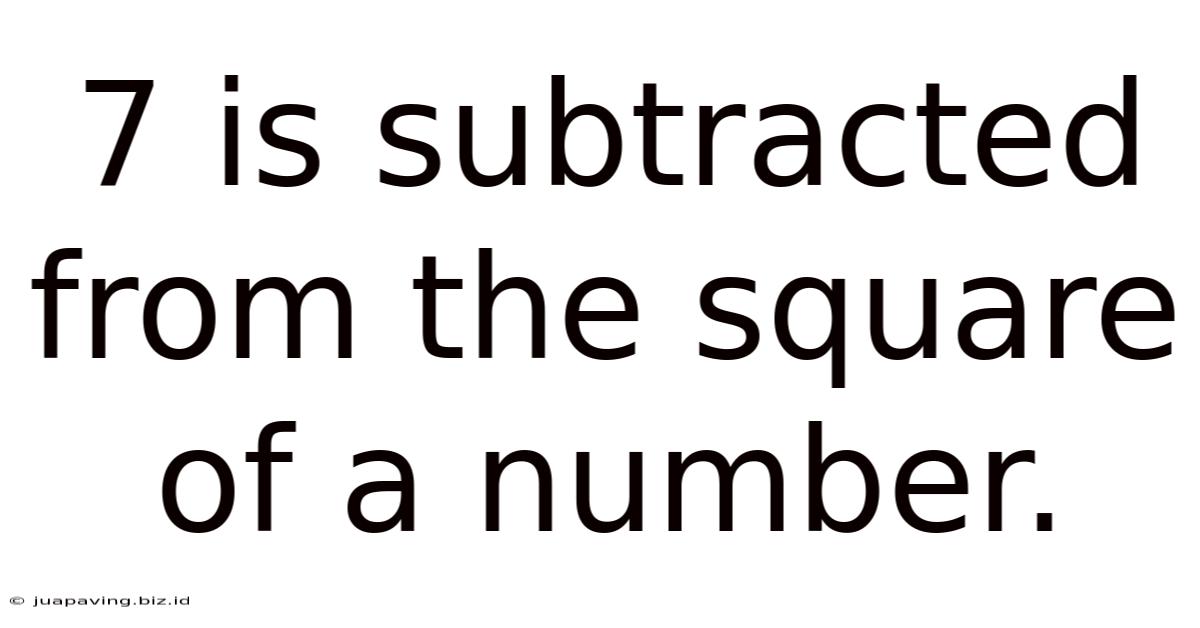
Table of Contents
7 Is Subtracted from the Square of a Number: A Deep Dive into Quadratic Equations and Their Applications
The seemingly simple phrase, "7 is subtracted from the square of a number," opens a door to a vast world of mathematical concepts, particularly within the realm of quadratic equations. This seemingly straightforward statement can lead us down a path exploring various algebraic manipulations, problem-solving techniques, and real-world applications. Let's delve into this fascinating mathematical journey.
Understanding the Core Concept
At its heart, the statement "7 is subtracted from the square of a number" translates directly into a mathematical equation. Let's represent the "number" with the variable x. Therefore, the equation becomes:
x² - 7
This is a quadratic expression, a polynomial of degree two. The power of two signifies the defining characteristic of quadratic expressions: they contain a variable raised to the power of two. The simplicity of this expression belies the complexity and richness it can unlock when explored further.
From Expression to Equation: Setting the Stage for Problem Solving
The expression x² - 7 alone doesn't pose a solvable problem. To create a problem, we need to set this expression equal to something. For instance, if we say "7 is subtracted from the square of a number, and the result is 18", we now have a solvable equation:
x² - 7 = 18
This transforms our quadratic expression into a quadratic equation, providing us with a concrete problem to solve. The solution will involve finding the value(s) of x that satisfy this equation.
Solving the Quadratic Equation: Multiple Approaches
Solving quadratic equations like x² - 7 = 18 involves several established methods. Let's explore some of the most common techniques:
1. Solving by Rearranging and Taking the Square Root
This method is particularly useful for simpler quadratic equations. The first step is to isolate the x² term:
x² - 7 = 18 becomes x² = 25
Then, we take the square root of both sides:
√x² = ±√25
This gives us two solutions:
x = 5 and x = -5
This illustrates a crucial point: quadratic equations often have two solutions. This is due to the fact that squaring a positive or a negative number results in a positive number.
2. Factoring the Quadratic Equation
Factoring is a powerful technique, especially when dealing with more complex quadratic equations. Let’s consider a slightly different scenario: "7 is subtracted from the square of a number, and the result is 0". This translates to:
x² - 7 = 0
This equation cannot be easily solved by taking the square root. However, we can factor it:
This equation can be factored as follows:
(x - √7)(x + √7) = 0
This gives us two solutions:
x = √7 and x = -√7
3. The Quadratic Formula: A Universal Solution
The quadratic formula is a powerful tool that can solve any quadratic equation of the form ax² + bx + c = 0. Our equation, x² - 7 = 18, can be rewritten in this standard form:
x² - 0x - 25 = 0
Where a = 1, b = 0, and c = -25.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values, we get:
x = [0 ± √(0² - 4 * 1 * -25)] / (2 * 1)
x = ±√100 / 2
x = ±10 / 2
x = ±5
This confirms the solutions we obtained using the simpler method. The quadratic formula guarantees a solution, even for equations that cannot be easily factored.
Exploring the Discriminant: Unveiling the Nature of Solutions
The expression b² - 4ac within the quadratic formula is called the discriminant. It provides valuable insight into the nature of the solutions:
- b² - 4ac > 0: The equation has two distinct real solutions (as in our examples).
- b² - 4ac = 0: The equation has one real solution (a repeated root).
- b² - 4ac < 0: The equation has no real solutions; the solutions are complex numbers (involving the imaginary unit i).
Understanding the discriminant is crucial for interpreting the results and anticipating the nature of solutions before even attempting to solve the equation.
Real-World Applications: Where Quadratic Equations Shine
The seemingly abstract concept of "7 is subtracted from the square of a number" finds surprising applications in numerous real-world scenarios. Here are a few examples:
1. Physics: Projectile Motion
The path of a projectile (like a ball thrown in the air) can be modeled using a quadratic equation. The equation describes the projectile's height as a function of time. Understanding the roots of this equation helps determine when the projectile reaches the ground.
2. Engineering: Designing Bridges and Buildings
Quadratic equations are fundamental to structural engineering. They are used to calculate the forces acting on structures, ensuring stability and safety. Archways and other curved structures often rely on quadratic relationships.
3. Economics: Modeling Revenue and Profit
In business, quadratic equations can model the relationship between the price of a product and the resulting revenue or profit. Finding the maximum point of a quadratic revenue function helps businesses optimize pricing strategies.
4. Computer Graphics: Creating Curves and Shapes
Quadratic equations are the building blocks of Bézier curves, commonly used in computer graphics to create smooth curves and shapes in designs and animations. Understanding these equations is essential for creating realistic and visually appealing graphics.
Expanding the Horizon: Variations and Extensions
The core concept can be extended to explore more complex scenarios. Instead of subtracting 7, we could add a different constant, multiply by a factor, or introduce additional terms. These variations lead to more intricate quadratic equations, demanding a more sophisticated understanding of algebraic manipulation and problem-solving techniques. For example, consider:
- 3x² - 7 = 18: This introduces a coefficient for the x² term.
- x² + 5x - 7 = 18: This introduces a linear term (5x).
- 2x² + 5x - 7 = 0: This presents a more standard quadratic equation requiring factoring or the quadratic formula.
Each variation presents unique challenges and opportunities to enhance your problem-solving skills.
Conclusion: A Journey of Mathematical Exploration
The simple statement, "7 is subtracted from the square of a number," serves as a gateway to a rich landscape of mathematical concepts and real-world applications. Through exploring different solution methods, understanding the discriminant, and examining real-world scenarios, we unravel the power and versatility of quadratic equations. This exploration underscores the importance of mathematical literacy and its crucial role in numerous scientific, engineering, and economic fields. The journey from a simple expression to a powerful tool highlights the beauty and practical utility of mathematics. As you delve deeper into the world of quadratic equations, you'll discover a wealth of knowledge and a profound appreciation for the elegance of mathematical problem-solving.
Latest Posts
Latest Posts
-
What Are The Functions Of Stem
May 12, 2025
-
What Is The Second Biggest Planet In Our Solar System
May 12, 2025
-
What Is The Definition Of Conclusion In Science
May 12, 2025
-
How Is Atp Made During Fermentation
May 12, 2025
-
Beyond The First Degree 7 Little Words
May 12, 2025
Related Post
Thank you for visiting our website which covers about 7 Is Subtracted From The Square Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.