6.012 As A Fraction In Simplest Form
Juapaving
May 11, 2025 · 5 min read
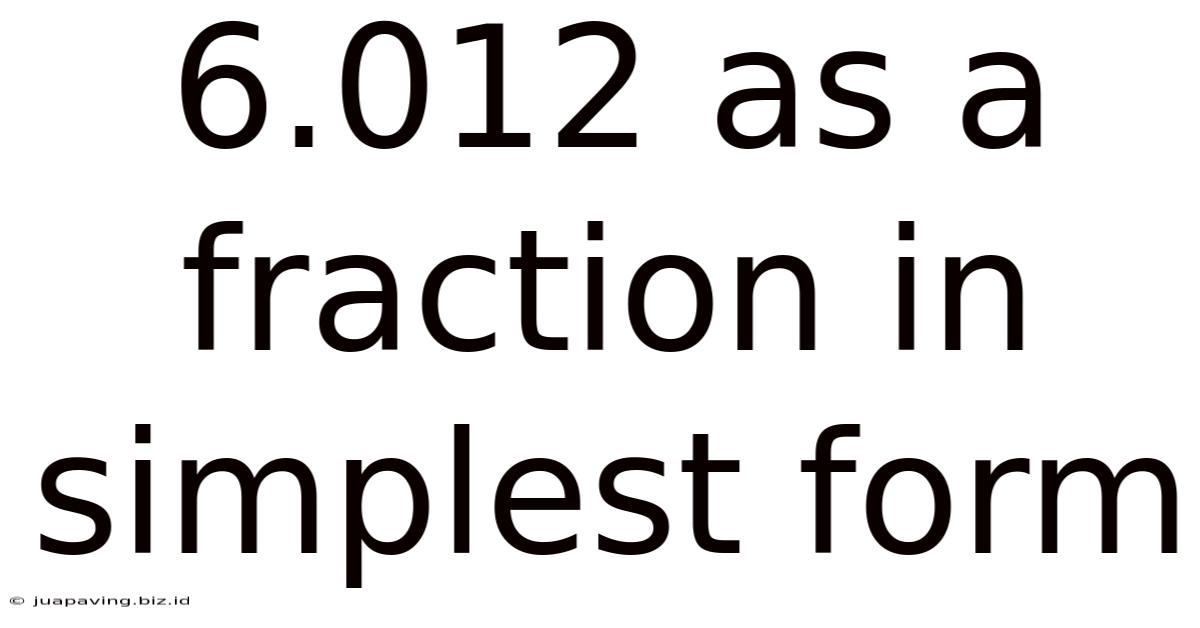
Table of Contents
6.012 as a Fraction in Simplest Form: A Comprehensive Guide
Converting decimal numbers to fractions might seem daunting at first, but with a systematic approach, it becomes a straightforward process. This article will guide you through converting the decimal 6.012 into its simplest fractional form, explaining each step in detail and providing helpful tips for similar conversions. We'll also explore the broader concept of decimal-to-fraction conversion and its applications.
Understanding Decimal Numbers and Fractions
Before diving into the conversion, let's refresh our understanding of decimal numbers and fractions.
-
Decimal Numbers: These numbers use a base-ten system, with digits placed to the left and right of a decimal point. The digits to the left represent whole numbers, while those to the right represent fractions of a whole (tenths, hundredths, thousandths, and so on).
-
Fractions: These numbers represent parts of a whole, expressed as a ratio of two integers: the numerator (top number) and the denominator (bottom number). For instance, 1/2 represents one part out of two equal parts.
Converting 6.012 to a Fraction: A Step-by-Step Guide
The key to converting a decimal to a fraction lies in understanding the place value of the decimal digits. Let's break down the conversion of 6.012:
Step 1: Identify the Place Value of the Last Digit
The last digit in 6.012 is 2, and it's in the thousandths place. This means our denominator will be 1000 (10 raised to the power of 3, as there are three digits after the decimal point).
Step 2: Write the Decimal as a Fraction
We can write 6.012 as a fraction with 1000 as the denominator:
6012/1000
Step 3: Simplify the Fraction
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator (6012) and the denominator (1000). The GCD is the largest number that divides both numbers without leaving a remainder. Finding the GCD can be done using various methods, including prime factorization or the Euclidean algorithm. For this example, we'll use prime factorization.
- Prime Factorization of 6012: 2 x 2 x 3 x 501
- Prime Factorization of 1000: 2 x 2 x 2 x 5 x 5 x 5
The common factors are 2 x 2 = 4.
Step 4: Divide Both Numerator and Denominator by the GCD
Dividing both the numerator and denominator by 4, we get:
1503/250
Therefore, the simplest fractional form of 6.012 is 1503/250.
Understanding the Concept of Greatest Common Divisor (GCD)
The GCD is crucial in simplifying fractions. It helps us reduce the fraction to its lowest terms, making it easier to understand and work with. Different methods exist to find the GCD, and choosing the most efficient method depends on the numbers involved.
-
Prime Factorization: This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power.
-
Euclidean Algorithm: This algorithm is particularly useful for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Practical Applications of Decimal-to-Fraction Conversion
Converting decimals to fractions is a fundamental skill with various applications in different fields:
-
Mathematics: It's essential for simplifying mathematical expressions, solving equations, and understanding relationships between numbers.
-
Engineering and Science: Precise measurements and calculations often require converting decimal values to fractions for accuracy and consistency.
-
Cooking and Baking: Recipes sometimes require precise measurements, and converting decimals to fractions ensures accuracy.
-
Finance: Working with money often involves fractions, especially when dealing with percentages, interest rates, and stock prices.
-
Construction: Accurate measurements and calculations are vital in construction, and converting decimals to fractions is crucial for precise work.
Handling Different Types of Decimal Numbers
The method described above applies to terminating decimals (decimals with a finite number of digits). However, some decimals are recurring or non-terminating (decimals that go on forever without repeating). Converting these to fractions requires a different approach.
-
Recurring Decimals: These decimals have a repeating pattern of digits after the decimal point. For instance, 0.333... (0.3 recurring) can be converted to the fraction 1/3. A systematic method involves using algebraic manipulation to solve for the fraction.
-
Non-Recurring Decimals: These decimals don't have a repeating pattern and go on infinitely. These numbers are often represented by irrational numbers like π (pi) or √2 (square root of 2). These cannot be expressed exactly as fractions. However, they can be approximated using fractions with a sufficient level of accuracy.
Advanced Techniques for Decimal-to-Fraction Conversion
For more complex decimals, advanced techniques might be needed:
-
Using a Calculator: Many calculators have a function to convert decimals to fractions directly.
-
Using Software: Various mathematical software packages and online tools can perform these conversions efficiently.
-
Continued Fractions: This advanced technique is particularly useful for converting non-terminating decimals into fractions that offer increasingly better approximations.
Conclusion
Converting 6.012 to its simplest fractional form, 1503/250, is a straightforward process involving understanding place values, identifying the greatest common divisor, and simplifying the resulting fraction. This skill has broad applications across various disciplines. Mastering this conversion, along with the concepts of decimals, fractions, and GCD, provides a solid foundation for further mathematical exploration and practical problem-solving. Remember to practice regularly to hone your skills and gain confidence in handling various types of decimal-to-fraction conversions. The ability to seamlessly convert between decimals and fractions enhances your mathematical proficiency and is valuable in numerous real-world contexts.
Latest Posts
Latest Posts
-
How Fast Is 90 Km H
May 13, 2025
-
List The 3 Principles Of Cell Theory
May 13, 2025
-
How Many Meters Are In A Decameter
May 13, 2025
-
What Is The Scientific Study Of Heredity Called
May 13, 2025
-
What Is The Acceleration Due To Gravity On The Moon
May 13, 2025
Related Post
Thank you for visiting our website which covers about 6.012 As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.