5 X 5 X 5 X 5 X 5
Juapaving
May 14, 2025 · 5 min read
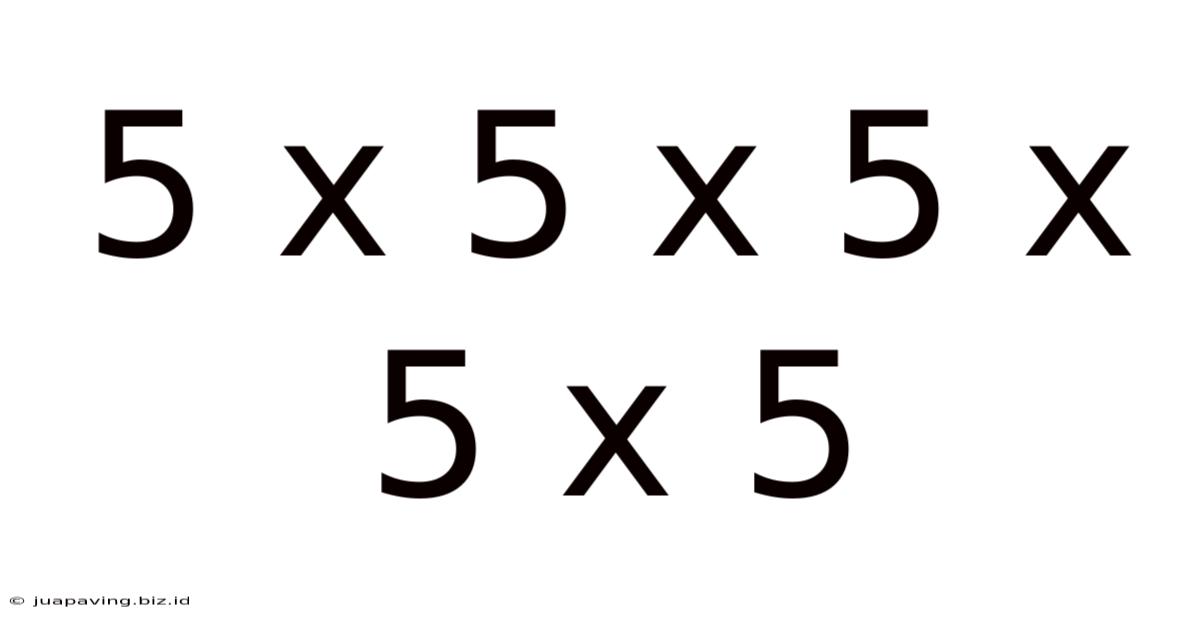
Table of Contents
Exploring the Mathematical Landscape of 5 x 5 x 5 x 5 x 5: A Deep Dive into Exponential Growth and its Applications
The seemingly simple mathematical expression, 5 x 5 x 5 x 5 x 5, or 5<sup>5</sup>, opens a door to a fascinating world of exponential growth, its implications in various fields, and the underlying principles of mathematics. This article delves into the calculation, explores its significance, and provides real-world examples to illustrate its practical applications.
Understanding the Fundamentals: Exponentiation
Before we embark on a detailed analysis of 5<sup>5</sup>, let's establish a foundational understanding of exponentiation. Exponentiation is a mathematical operation that involves raising a number (the base) to a power (the exponent). In our case, 5 is the base, and 5 is the exponent. This means we multiply the base by itself the number of times indicated by the exponent.
The Calculation of 5<sup>5</sup>
Calculating 5<sup>5</sup> is straightforward:
5 x 5 x 5 x 5 x 5 = 3125
This simple calculation reveals a significant increase from the initial base number. This rapid growth is characteristic of exponential functions and is the subject of much study in mathematics and various scientific disciplines.
Exploring the Significance of Exponential Growth
The result, 3125, represents the power of exponential growth. Starting with a relatively small base number (5), repeated multiplication leads to a substantial increase. This concept is crucial in understanding many natural phenomena and technological advancements.
Exponential Growth in Nature
Exponential growth is prevalent in the natural world. Consider the following examples:
-
Bacterial growth: Under ideal conditions, bacteria reproduce exponentially. A single bacterium can divide into two, then four, then eight, and so on, resulting in a rapid increase in population. This principle is crucial in understanding infectious diseases and the importance of controlling bacterial growth.
-
Population growth: Uncontrolled population growth in any species follows an exponential pattern. The larger the population, the faster it grows, leading to potential resource depletion and ecological imbalances. Understanding exponential growth is essential for effective population management.
-
Compound interest: The power of compound interest is a testament to exponential growth. The interest earned in each period is added to the principal, leading to exponentially increasing returns over time. This concept is fundamental in personal finance and investment strategies.
Exponential Growth in Technology and Science
Exponential growth is also a defining characteristic of many technological advancements and scientific discoveries:
-
Moore's Law: This observation states that the number of transistors on a microchip doubles approximately every two years. This exponential increase in computing power has driven the rapid advancement of technology and the digital revolution.
-
Network effects: The value of many networks, such as social media platforms or communication systems, increases exponentially with the number of users. The more users there are, the more valuable the network becomes, attracting even more users. This positive feedback loop fuels exponential growth.
-
Data growth: The amount of digital data generated globally is growing exponentially. This necessitates the development of advanced storage and processing technologies to handle the ever-increasing volume of information.
Beyond the Calculation: Applications of 5<sup>5</sup>
While the calculation of 5<sup>5</sup> = 3125 is simple, its applications extend far beyond a basic arithmetic problem. Consider these examples:
-
Combinatorics: If you have 5 options for each of 5 independent choices, the total number of possible combinations is 5<sup>5</sup> = 3125. This principle is fundamental in probability and statistics, used in scenarios from lottery calculations to genetic combinations.
-
Geometry: Imagine a 5 x 5 x 5 cube. The number of unit cubes within this larger cube is 5<sup>3</sup> = 125. While not directly 5<sup>5</sup>, this illustrates the principle of exponential volume increase in three-dimensional space. Extending this concept further to higher dimensions can showcase exponential scaling in more complex geometric systems.
-
Computer Science: In computer science, 5<sup>5</sup> could represent the number of possible states in a system with 5 components, each having 5 possible states. This is important in algorithm design, state machine analysis, and complexity calculations.
Practical Exercises and Further Exploration
To solidify your understanding of exponential growth and the significance of 5<sup>5</sup>, consider the following exercises:
-
Compare Growth: Compare the growth of 5<sup>5</sup> to the growth of 5 x 5 (5<sup>2</sup>). Analyze the difference and explain the accelerating nature of exponential growth.
-
Real-world application: Identify a real-world example of exponential growth, either from nature or technology. Explain how the principles of exponential growth affect this example.
-
Exploring Larger Exponents: Calculate 5<sup>6</sup>, 5<sup>7</sup>, and 5<sup>8</sup>. Observe the increasingly rapid growth and visualize the implications of such rapid expansion. Consider how this applies to issues like climate change or technological singularity.
-
Graphing Exponential Functions: Create a graph depicting the exponential function y = 5<sup>x</sup> for values of x from 0 to 5. Observe the shape of the curve and how it illustrates exponential growth.
Conclusion: The Enduring Importance of 5<sup>5</sup>
The seemingly simple calculation of 5 x 5 x 5 x 5 x 5 = 3125 provides a gateway to understanding the profound implications of exponential growth. From natural phenomena to technological advancements, exponential growth shapes our world in countless ways. By grasping the fundamentals of exponentiation and exploring its practical applications, we can better comprehend the complexities of the world around us and make informed decisions in various fields. Further exploration into exponential functions and their related mathematical concepts will only deepen this understanding, leading to new insights and innovative solutions. Remember that even seemingly simple mathematical expressions can reveal profound truths about the universe and our place within it.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about 5 X 5 X 5 X 5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.