5 6 Divided By 1 12
Juapaving
May 13, 2025 · 5 min read
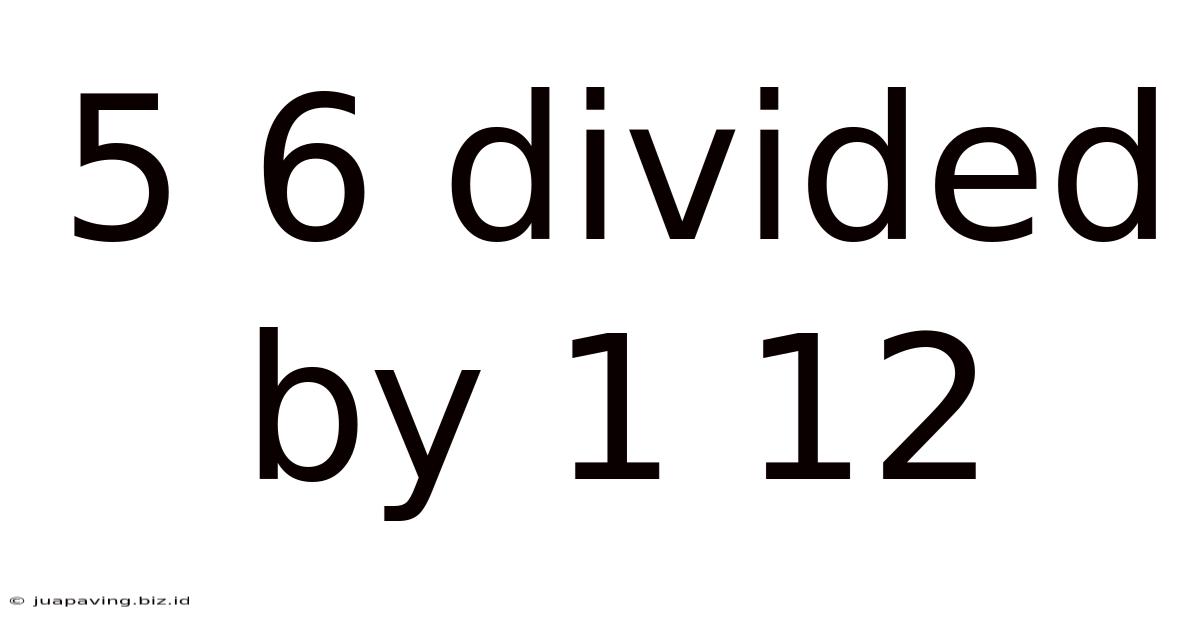
Table of Contents
Deconstructing the Division: 5 6/1 12 and the Art of Fraction Division
The seemingly simple problem of dividing 5 6 by 1 12 might seem straightforward at first glance. However, a deeper dive reveals a rich tapestry of mathematical concepts, offering a wonderful opportunity to explore the intricacies of fraction division and its practical applications. This comprehensive guide will not only solve the problem but also illuminate the underlying principles, providing you with the tools to tackle similar challenges with confidence.
Understanding Mixed Numbers and Improper Fractions
Before embarking on the division itself, let's solidify our understanding of the components involved. The numbers "5 6" and "1 12" are mixed numbers. A mixed number combines a whole number and a fraction. To perform division effectively, we need to convert these mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Converting 5 6 to an improper fraction:
- Multiply the whole number (5) by the denominator (6): 5 * 6 = 30
- Add the numerator (6): 30 + 6 = 36
- Keep the same denominator (6): The improper fraction is 36/6
Converting 1 12 to an improper fraction:
- Multiply the whole number (1) by the denominator (12): 1 * 12 = 12
- Add the numerator (12): 12 + 12 = 24
- Keep the same denominator (12): The improper fraction is 24/12
The Mechanics of Fraction Division: Inverting and Multiplying
Now that we have converted our mixed numbers into improper fractions, we can proceed with the division. The core principle of dividing fractions is to invert the second fraction (the divisor) and multiply. This process is also known as multiplying by the reciprocal.
Step-by-step solution:
-
Rewrite the problem: The problem 5 6 ÷ 1 12 becomes (36/6) ÷ (24/12).
-
Invert the second fraction: The reciprocal of 24/12 is 12/24.
-
Multiply the fractions: (36/6) * (12/24) = (36 * 12) / (6 * 24)
-
Simplify: Before multiplying, we can simplify the expression by canceling common factors. Notice that 12 is a factor of both 12 and 24, and 6 is a factor of both 36 and 24. Let's simplify:
(36/6) * (12/24) = (6/1) * (1/2) = 6/2
-
Final Answer: 6/2 simplifies to 3. Therefore, 5 6 ÷ 1 12 = 3
Exploring Different Approaches: A Deeper Mathematical Dive
While the method above is efficient and widely used, let's explore alternative approaches to further solidify our understanding.
Method 2: Decimal Conversion
Another way to tackle this problem is to convert the mixed numbers into decimals before performing the division.
- 5 6 = 5.6
- 1 12 = 1.12
Now we perform the decimal division: 5.6 ÷ 1.12 = 5
This method offers a different perspective, highlighting the interchangeability between fractions and decimals. However, this method can sometimes lead to inaccuracies due to rounding errors, especially when dealing with repeating decimals.
Method 3: Understanding the Concept of Division
Division can be conceptually understood as asking, "How many times does the divisor fit into the dividend?" In our case, we're asking, "How many times does 1 12 fit into 5 6?" To illustrate this visually, imagine you have 5 and 6/6 (which equals 6 units), and you want to divide them into groups of 1 and 12/12 (which equals 2 units). Intuitively, you can see that you would have 3 complete groups. This method aids in building an intuitive understanding of the concept.
Practical Applications of Fraction Division
The ability to divide fractions is not limited to abstract mathematical exercises. It finds widespread application in various real-world scenarios:
-
Baking and Cooking: Scaling recipes up or down requires accurate fraction division. For example, if a recipe calls for 1 1/2 cups of flour and you want to make half the recipe, you'll need to divide 1 1/2 by 2.
-
Sewing and Tailoring: Calculating fabric requirements for garments involves working with fractional measurements and division.
-
Construction and Engineering: Accurate measurements and calculations involving fractions are vital in construction projects, ensuring precision and structural integrity.
-
Finance and Budgeting: Dividing budgets or resources among different projects or individuals frequently involves fractions.
-
Data Analysis and Statistics: Working with datasets and calculating averages or proportions frequently involves fraction division and manipulation.
Mastering Fraction Division: Tips and Tricks
While the basic principles of fraction division are relatively straightforward, mastering the process requires practice and attention to detail. Here are some useful tips:
-
Practice regularly: Consistent practice is key to building proficiency and confidence.
-
Master simplification: Simplifying fractions before multiplication significantly reduces the complexity of calculations.
-
Check your work: Always double-check your calculations to avoid errors.
-
Use visual aids: Visual aids such as diagrams or models can help to understand the concept of fraction division, particularly for beginners.
-
Understand the context: Always consider the context of the problem, which helps in interpreting the results meaningfully.
-
Explore different methods: Familiarity with multiple methods enhances your problem-solving capabilities.
Conclusion: Beyond the Numbers
The seemingly simple problem of 5 6 divided by 1 12 has provided a springboard for exploring a wide range of mathematical concepts. From converting mixed numbers to improper fractions, to mastering the mechanics of fraction division, and understanding its practical applications, we've covered a significant amount of ground. Remember that mathematics is not just about numbers; it's about understanding the underlying principles and applying them to solve real-world problems effectively. By mastering fraction division, you've not only solved a specific problem, but you've also equipped yourself with a valuable tool for various aspects of life and work. Continuous learning and practice will further hone your skills, making you more confident and adept in your mathematical endeavors.
Latest Posts
Latest Posts
-
Simplify The Square Root Of 30
May 13, 2025
-
Is 32 A Prime Number Or A Composite Number
May 13, 2025
-
How Many Diagonals Are In An Octagon
May 13, 2025
-
Is Kcl An Acid Or A Base
May 13, 2025
-
5 Letter Words Containing E R
May 13, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 1 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.