5 3 5x 2 4 7 3x 1
Juapaving
May 10, 2025 · 5 min read
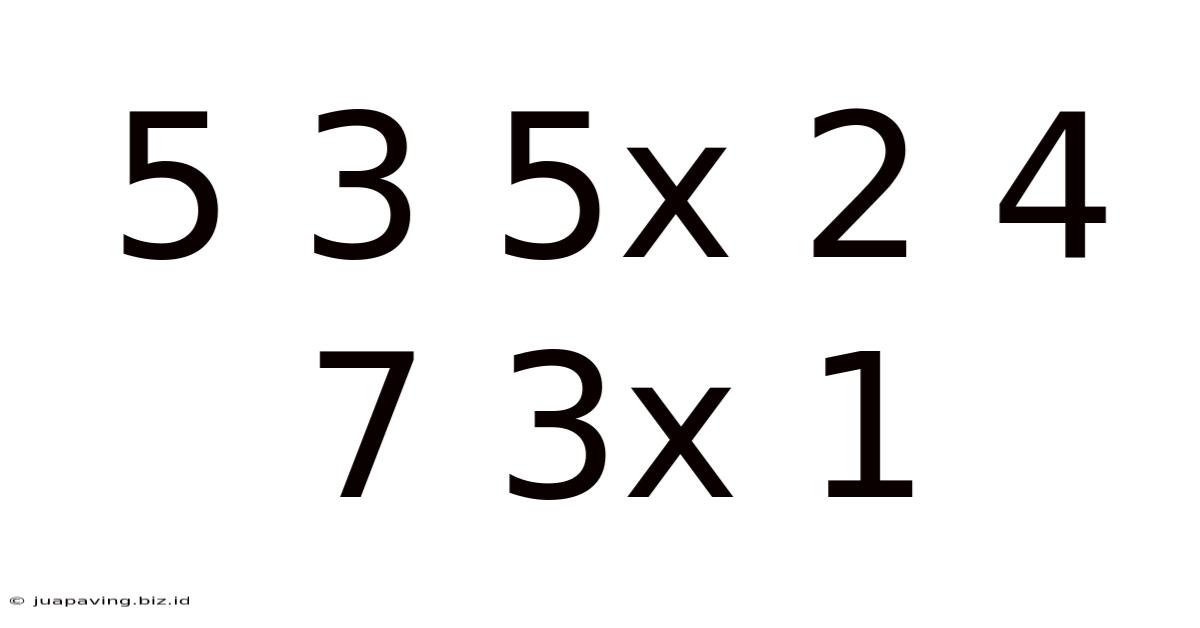
Table of Contents
Decoding the Sequence: 5 3 5x 2 4 7 3x 1 – A Deep Dive into Pattern Recognition and Mathematical Puzzles
The seemingly innocuous sequence "5 3 5x 2 4 7 3x 1" presents a fascinating challenge for those interested in pattern recognition, mathematical puzzles, and the art of logical deduction. This article will explore various approaches to decipher this sequence, examining potential patterns, underlying mathematical relationships, and the broader implications for solving similar numerical puzzles. We'll delve into different methodologies, from simple arithmetic operations to more advanced concepts, ultimately aiming to uncover the "secret code" hidden within these numbers.
Understanding the Nature of the Problem
Before jumping into solutions, it's crucial to define the problem. The sequence "5 3 5x 2 4 7 3x 1" is ambiguous. The presence of "x" isn't clearly defined. Does "x" represent multiplication? An unknown variable? A placeholder for a different operation? This ambiguity opens up multiple avenues for interpretation and solution. We'll explore several possibilities, acknowledging that there might not be a single "correct" answer. The beauty of such puzzles lies in the exploration of different logical paths.
Approach 1: Treating "x" as Multiplication
Let's initially assume that "x" signifies multiplication. This is a common interpretation in mathematical sequences. The sequence then becomes: 5, 3, 5 * 2, 4, 7, 3 * 1. This simplifies to: 5, 3, 10, 4, 7, 3.
Even with this simplification, a clear pattern isn't immediately evident. We can explore several avenues:
Subsequence Analysis:
- Odd vs. Even Numbers: Observing the alternating pattern of odd and even numbers doesn't provide a readily apparent rule.
- Differences between Consecutive Numbers: Calculating the differences between adjacent numbers (2, 7, -6, 3, -4) yields no consistent pattern.
- Prime Numbers: Examining the prime numbers within the sequence (3, 5, 7) doesn't offer a straightforward connection to the other elements.
More Advanced Approaches:
Without a clear arithmetical pattern, we might consider more complex mathematical relationships. Perhaps the sequence is based on:
- Modular Arithmetic: Examining remainders when divided by a specific number could reveal hidden relationships. However, testing various moduli doesn't immediately produce a consistent outcome.
- Fibonacci-like Sequences: While this sequence doesn't directly follow a Fibonacci sequence (where each number is the sum of the two preceding ones), exploring variations or modifications of Fibonacci patterns might yield clues. This could involve adding, subtracting, or multiplying terms in different combinations.
- Polynomial Relationships: It's possible that the numbers are derived from a polynomial equation. Finding the correct polynomial would require solving a system of equations, which could be challenging without additional information.
Approach 2: "x" as an Unknown Variable
If "x" represents an unknown variable, the problem becomes significantly more complex. We now have a series of equations rather than a simple sequence. To solve for "x," we'd need additional information or constraints. We could explore different scenarios:
- Assuming a linear relationship: We could try to fit a linear equation to the data points, but this would likely result in multiple potential solutions and require additional context.
- System of Equations: If we assume a relationship between consecutive numbers involving "x," we could set up a system of equations. However, without further constraints or equations, this system would be underdetermined, leading to an infinite number of solutions.
Approach 3: "x" as a Placeholder for a Different Operation
Perhaps "x" is a placeholder for a completely different operation, such as addition, subtraction, or even a more complex mathematical function. This requires a more creative and exploratory approach. We could hypothesize different operations and test their feasibility. For instance:
- Alternating Operations: We could try alternating addition and subtraction, or multiplication and division. However, this doesn't immediately lead to a clear and consistent pattern.
- Combination of Operations: A more complex solution might involve a combination of various operations, perhaps following a specific rule or algorithm based on the position of the numbers in the sequence.
Exploring Beyond Arithmetic: Considering Other Possibilities
Given the challenges of finding a purely numerical solution, we could explore alternative interpretations:
- Encoding: Is this sequence a form of encoding or cryptography? Could the numbers represent letters of the alphabet, musical notes, or elements from another system? This necessitates exploring different encoding schemes and their potential mappings.
- Geometric Patterns: Are there underlying geometric patterns related to these numbers? Could they represent coordinates, lengths, or areas in a specific geometrical configuration?
- External Context: The puzzle's solution might depend on external context or additional information that's not provided. Perhaps the sequence is part of a larger problem or a riddle with hidden clues.
Conclusion: The Importance of Pattern Recognition and Problem-Solving Strategies
The sequence "5 3 5x 2 4 7 3x 1" serves as a prime example of a seemingly simple puzzle that can quickly become complex. The ambiguity of "x" opens up a wide range of possible interpretations and solutions. Solving such puzzles requires a multifaceted approach, encompassing:
- Systematic Exploration: Trying various methods systematically, from simple arithmetic to more advanced mathematical techniques.
- Creative Thinking: Imagining different interpretations of "x" and exploring non-traditional approaches.
- Logical Deduction: Carefully analyzing patterns, relationships, and potential constraints.
- Persistence and Patience: Recognizing that the solution might not be immediate and requiring perseverance.
While this article doesn't offer a single definitive answer, the process of exploring these different approaches highlights the importance of developing strong pattern recognition skills and a flexible problem-solving mindset. This puzzle serves as a valuable exercise in logical reasoning and encourages a deeper appreciation for the beauty and complexity hidden within seemingly simple numerical sequences. The ultimate goal is not necessarily finding the "correct" answer (as it may be subjective depending on the interpretation of "x"), but rather, enhancing our analytical and problem-solving capabilities. The journey of exploration and deduction is just as rewarding as the destination.
Latest Posts
Latest Posts
-
What Is The Name Of The Process
May 10, 2025
-
Which Of The Following Is A Secondary Sex Characteristic
May 10, 2025
-
Light Speed In Km Per Hour
May 10, 2025
-
Function Of The Gizzard In An Earthworm
May 10, 2025
-
Why Does Moon Have No Atmosphere
May 10, 2025
Related Post
Thank you for visiting our website which covers about 5 3 5x 2 4 7 3x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.