35 Out Of 40 In Percentage
Juapaving
May 14, 2025 · 4 min read
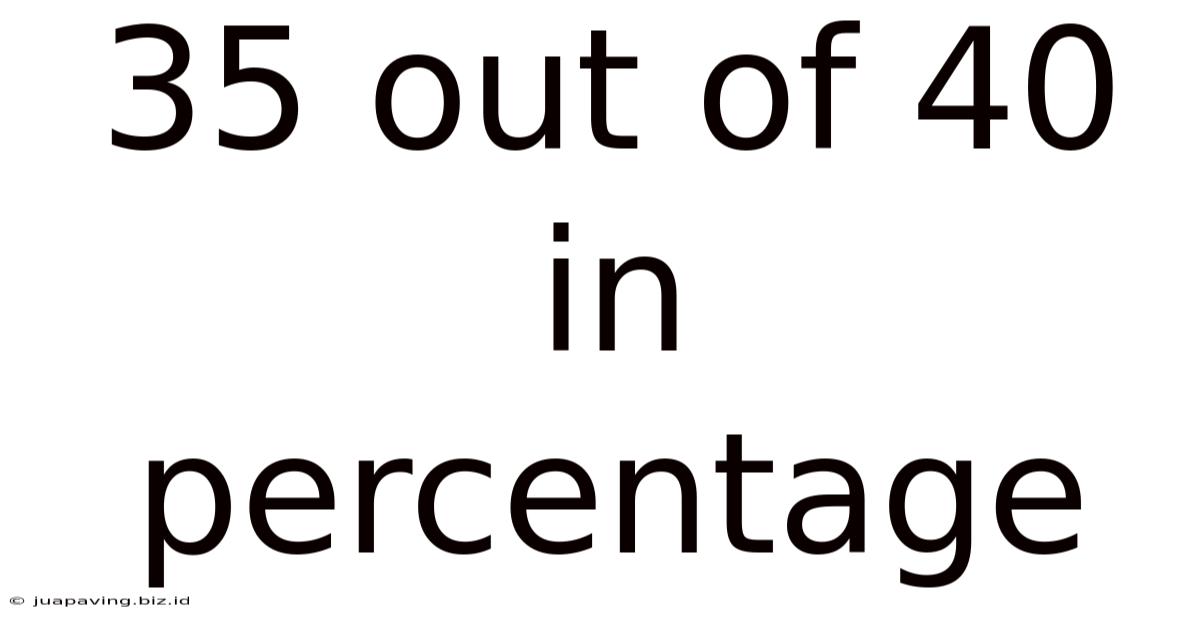
Table of Contents
35 out of 40 in Percentage: A Comprehensive Guide to Understanding and Calculating Percentages
Calculating percentages is a fundamental skill applicable across various fields, from academic assessments to financial transactions. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating results effectively. This comprehensive guide will delve into the intricacies of calculating 35 out of 40 as a percentage, exploring different methods and highlighting their applications. We'll also explore related percentage calculations and provide practical examples to solidify your understanding.
Understanding the Basics of Percentage Calculations
Before we tackle the specific calculation of 35 out of 40, let's refresh our understanding of percentages. A percentage represents a fraction of 100. The term "percent" literally means "per hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
Calculating 35 out of 40 as a Percentage: Step-by-Step Guide
Now, let's apply this formula to calculate 35 out of 40 as a percentage. In this case:
- Part: 35 (the number of correct answers, successful attempts, or any other relevant part)
- Whole: 40 (the total number of items, attempts, or the overall total)
-
Divide the part by the whole: 35 / 40 = 0.875
-
Multiply the result by 100%: 0.875 * 100% = 87.5%
Therefore, 35 out of 40 is 87.5%.
Different Methods for Calculating Percentages
While the above method is the most straightforward, there are alternative approaches to calculating percentages, particularly useful depending on the context and your comfort level with mathematical operations.
Method 2: Using Proportions
You can also solve this using proportions. We can set up a proportion:
35/40 = x/100
To solve for x (the percentage), we cross-multiply:
40x = 3500
x = 3500 / 40
x = 87.5
Therefore, x = 87.5%, confirming our previous calculation.
Method 3: Simplifying the Fraction First
Sometimes, simplifying the fraction before converting to a percentage can make the calculation easier. In this case:
35/40 can be simplified by dividing both the numerator and denominator by 5:
7/8
Now, convert the simplified fraction to a percentage:
7 / 8 = 0.875
0.875 * 100% = 87.5%
Practical Applications and Interpretations of 87.5%
The result of 87.5% can be interpreted in various contexts. Let's explore some examples:
-
Academic Performance: If 35 out of 40 represents a test score, 87.5% indicates a very good performance, suggesting a strong understanding of the subject matter.
-
Project Completion: If 35 out of 40 tasks are completed, 87.5% signifies significant progress on the project. Only a small portion remains unfinished.
-
Survey Results: If 35 out of 40 respondents answered positively to a survey question, 87.5% represents a strong positive response rate.
-
Sales Targets: If 35 out of 40 sales targets are met, 87.5% shows a high achievement rate.
Related Percentage Calculations and Problem Solving
Understanding the calculation of 35 out of 40 allows us to tackle similar percentage problems. For instance, you can easily adapt the formula to calculate:
-
What is 87.5% of 40? (Answer: 35)
-
What percentage is 30 out of 40? (Answer: 75%)
-
If a score of 35 out of 40 represents 87.5%, what score would represent 90%? (This requires a bit more calculation – we'd need to find 90% of 40 which is 36)
Beyond the Basics: Advanced Percentage Concepts and Applications
While calculating 35 out of 40 is a relatively straightforward percentage calculation, understanding percentages extends far beyond simple conversions. Here are some advanced concepts and applications:
-
Percentage Change: Calculating the percentage increase or decrease between two values. This is commonly used in finance to track changes in stock prices, profits, or expenses.
-
Compound Interest: Understanding how interest accrues over time, compounding on both the principal and accumulated interest. This is crucial for understanding investments and loan repayments.
-
Percentage Points: A subtle but important distinction between percentage change and percentage points. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage.
-
Statistical Significance: Using percentages to determine the probability of an event occurring and assess the reliability of research findings.
Conclusion: Mastering Percentage Calculations for Real-World Success
Mastering percentage calculations is a vital skill that enhances your ability to interpret data, make informed decisions, and communicate effectively across diverse fields. By understanding the basic formula, exploring different calculation methods, and applying these principles to real-world scenarios, you can confidently navigate various situations requiring percentage analysis. The example of calculating 35 out of 40 as a percentage provides a strong foundation for tackling more complex percentage-based problems. Remember to practice regularly to reinforce your understanding and build your proficiency. The ability to accurately calculate and interpret percentages is a valuable asset in both personal and professional contexts, contributing to greater understanding and informed decision-making.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about 35 Out Of 40 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.