33 4 As A Mixed Number
Juapaving
May 12, 2025 · 5 min read
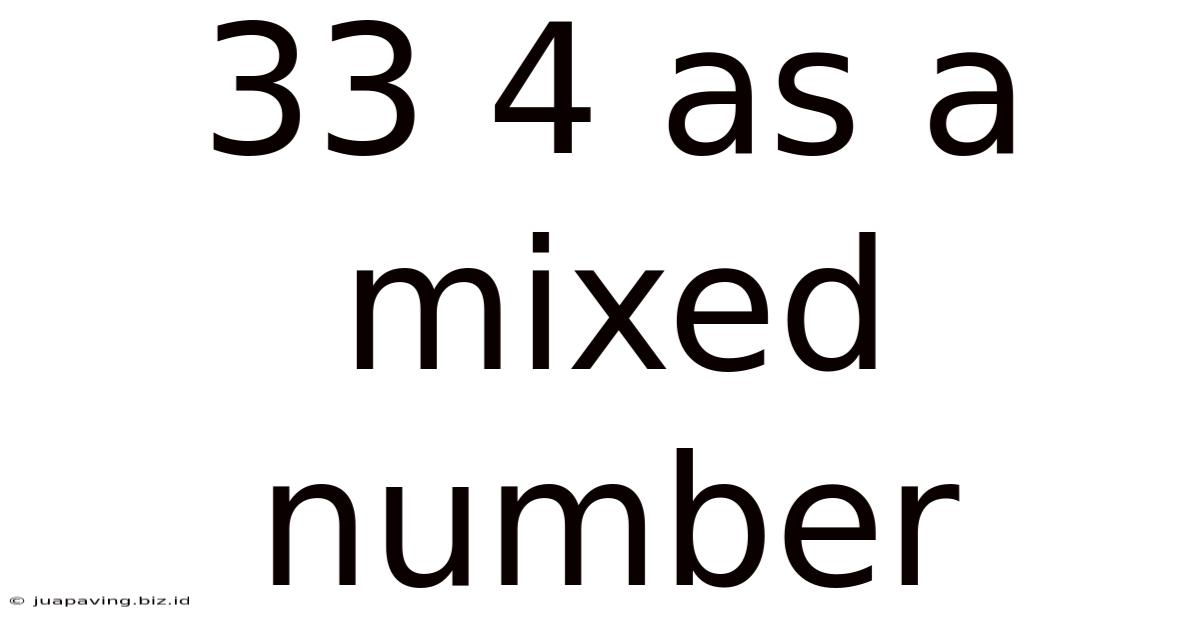
Table of Contents
33/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversions is fundamental to mathematics. This comprehensive guide delves into the process of converting the improper fraction 33/4 into a mixed number, exploring the underlying concepts and providing practical examples. We'll also examine why this conversion is important and its applications in various fields.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). For example, 1 ¾, 2 ⅔, and 5 ⅛ are all mixed numbers. They represent a quantity greater than one whole unit.
What is an Improper Fraction?
An improper fraction, conversely, has a numerator that is equal to or greater than its denominator. Examples include 7/4, 11/5, and of course, our subject of focus: 33/4. These fractions represent a quantity equal to or greater than one whole unit.
Converting 33/4 to a Mixed Number: The Step-by-Step Process
Converting an improper fraction like 33/4 to a mixed number involves dividing the numerator by the denominator. Here's a detailed breakdown:
-
Divide the Numerator by the Denominator: We start by dividing 33 (the numerator) by 4 (the denominator).
33 ÷ 4 = 8 with a remainder of 1.
-
Identify the Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In our case, the quotient is 8.
-
Determine the Remainder: The remainder from the division becomes the numerator of the fractional part of the mixed number. Our remainder is 1.
-
Keep the Original Denominator: The denominator of the fractional part remains the same as the original denominator. It stays as 4.
-
Combine the Whole Number and the Fraction: Finally, we combine the whole number and the fraction to form the mixed number.
Therefore, 33/4 = 8 ⅛
Visual Representation: Understanding the Conversion
Imagine you have 33 quarters. A quarter is a representation of ¼. To understand the conversion to a mixed number, you would group these quarters into sets of four (because the denominator is 4). You can form eight complete sets of four quarters (representing eight whole units, the whole number part of the mixed number) with one quarter left over. This leftover quarter is the fraction part: ⅛.
Why is this Conversion Important?
Converting improper fractions to mixed numbers is crucial for several reasons:
-
Easier Comprehension: Mixed numbers are generally easier to understand and visualize than improper fractions. It's simpler to grasp the concept of "8 and a quarter" than "thirty-three fourths."
-
Real-World Applications: Many real-world situations require the use of mixed numbers. Imagine measuring ingredients for a recipe, calculating distances, or dividing resources. Mixed numbers offer a more practical and intuitive representation of these quantities.
-
Mathematical Operations: While performing certain mathematical operations (like addition and subtraction of fractions), using mixed numbers can sometimes simplify the calculations, although converting back to improper fractions might be necessary depending on the operation.
Further Exploration: Working with Other Improper Fractions
The method outlined above applies to any improper fraction. Let's consider a few more examples:
-
Converting 22/5:
22 ÷ 5 = 4 with a remainder of 2.
Therefore, 22/5 = 4 ⅖
-
Converting 17/3:
17 ÷ 3 = 5 with a remainder of 2.
Therefore, 17/3 = 5 ⅔
-
Converting 45/8:
45 ÷ 8 = 5 with a remainder of 5.
Therefore, 45/8 = 5 ⅝
These examples highlight the consistent application of the division method to transform any improper fraction into its mixed number equivalent.
Practical Applications in Different Fields
The conversion of improper fractions to mixed numbers has wide-ranging applications in diverse fields:
-
Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities, providing a clear and practical measurement. Understanding the conversion allows for accurate ingredient measurements.
-
Construction and Engineering: Precise measurements are essential in these fields. Mixed numbers are frequently used in blueprints and specifications, ensuring accuracy in construction projects.
-
Finance and Accounting: Calculations involving fractional shares or portions of assets are often expressed using mixed numbers for better understanding and clarity.
-
Time Measurement: Time is often expressed using mixed numbers, such as 2 ½ hours or 1 ¼ minutes.
-
Data Analysis and Statistics: When dealing with fractional data points, using mixed numbers can aid in interpretation and presentation.
Troubleshooting Common Mistakes
While converting improper fractions to mixed numbers is relatively straightforward, some common mistakes should be avoided:
-
Incorrect Division: Ensure accurate division of the numerator by the denominator. Even a small mistake in division will lead to an incorrect mixed number.
-
Misplacing the Remainder: The remainder is crucial. Make sure it correctly becomes the numerator of the fractional part.
-
Ignoring or Changing the Denominator: The denominator remains unchanged throughout the conversion process.
-
Failing to Simplify: After obtaining the mixed number, ensure the fractional part is in its simplest form (reduced to the lowest terms).
Conclusion: Mastering the Conversion
Converting improper fractions to mixed numbers is a fundamental skill in mathematics. This guide has provided a comprehensive understanding of the process, accompanied by examples and practical applications. Mastering this conversion strengthens mathematical proficiency and facilitates a clear understanding of quantities in various real-world scenarios. Remember the simple steps: divide, identify the whole number, determine the remainder, and combine to form the mixed number. With practice, this conversion will become second nature, empowering you to confidently tackle any improper fraction. By understanding and applying this concept, you enhance your problem-solving abilities across diverse applications.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about 33 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.