3 Geometric Solids Which Have Circular Cross Sections
Juapaving
Apr 04, 2025 · 6 min read
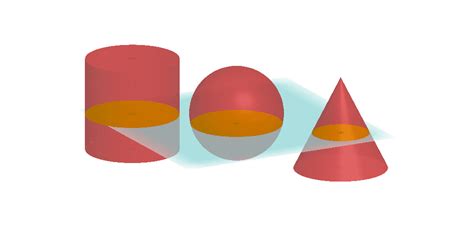
Table of Contents
3 Geometric Solids Which Have Circular Cross Sections: A Deep Dive
Geometric solids, three-dimensional shapes, offer a fascinating realm of exploration in mathematics and beyond. Understanding their properties, especially their cross-sections, provides crucial insights into their volume, surface area, and applications in various fields. This article delves into three specific geometric solids that consistently produce circular cross-sections when sliced: the cylinder, the cone, and the sphere. We'll examine their unique characteristics, explore their real-world applications, and discuss the mathematical principles underpinning their circular cross-sections.
1. The Cylinder: A Timeless Shape with Consistent Circles
The cylinder, a ubiquitous shape in everyday life, is defined by its two parallel circular bases connected by a curved lateral surface. This simple yet elegant shape boasts a remarkable consistency when it comes to cross-sections.
Understanding Cylindrical Cross-Sections
Regardless of how you slice a cylinder (parallel to the base, perpendicular to the base, or at an angle), as long as the cut passes through the lateral surface, you will invariably obtain a circular cross-section.
-
Parallel to the Base: A slice parallel to the circular bases results in a cross-section that is an identical circle, mirroring the bases themselves. This is intuitively obvious – you're essentially creating a smaller, scaled-down version of the original cylinder.
-
Perpendicular to the Base: Cutting perpendicular to the bases yields a rectangular cross-section. However, within that rectangle, the curved lateral surface of the cylinder forms a perfectly circular cross-section. This is because the circular nature of the base is preserved along the cylinder's height.
-
Angled Cross-Sections: Even with angled cuts, the cross-section remains circular. Imagine slicing through the cylinder at a diagonal; the resulting shape will be an ellipse. However, if you look closely, the intersection of the plane (the cut) and the curved lateral surface continues to form a perfect circle, albeit situated within the ellipse. This is a crucial aspect illustrating the fundamental circular nature inherent to the cylindrical structure.
Real-World Applications of Cylinders
The consistent circular cross-sections of cylinders make them exceptionally practical in various applications:
-
Engineering: Cylindrical pipes, shafts, and columns rely on this consistent strength and structural integrity derived from their circular cross-sections. The even distribution of stress in circular cross-sections allows cylinders to bear substantial loads without buckling or collapsing.
-
Packaging: Cylindrical containers (cans, bottles, tubes) are cost-effective and efficient to manufacture, stack, and transport because of their uniform shape and consistent circular profile.
-
Manufacturing: Lathes and other machining tools often utilize cylindrical forms to create other components with precision. The predictable nature of the circular cross-section simplifies the manufacturing process.
-
Everyday Objects: From drinking glasses to batteries to candles, cylinders are everywhere, highlighting their versatility and practical design.
2. The Cone: Circular Cross-Sections from Apex to Base
A cone, characterized by a circular base and a single apex point, also exhibits fascinating circular cross-sectional properties. While not as consistently circular as the cylinder, certain types of cuts consistently yield circular cross-sections.
Understanding Conical Cross-Sections
The key to understanding conical cross-sections lies in the orientation of the cutting plane.
-
Parallel to the Base: Slicing a cone parallel to its base yields a smaller, similar cone – a smaller circle. This smaller cone shares the same apex as the original cone, but with a reduced circular base. The cross-section of this smaller cone is, of course, a circle.
-
Perpendicular to the Base Through the Apex: Cutting through the apex and perpendicular to the base results in an isosceles triangle. While not a circle, the intersection of this cut with the cone's curved surface exhibits a point and a line segment.
-
Other Cross-Sections: Other angled cuts through the cone will result in ellipses, parabolas, or hyperbolas – the conic sections. However, these cuts do not consistently produce circles.
Real-World Applications of Cones
Despite not having uniformly circular cross-sections in every orientation, cones still play significant roles in various applications.
-
Traffic Cones: Their iconic shape acts as a visual marker and its stability is partly derived from its conical geometry.
-
Ice Cream Cones: The cone's shape is ideal for holding and containing ice cream.
-
Funnels: The gradual narrowing of the cone facilitates efficient transfer of liquids.
-
Architectural Structures: Certain architectural elements incorporate conical shapes for both aesthetic and structural purposes.
The predictable nature of parallel cross-sections in a cone is essential in applications where scaled versions of the cone are needed, such as in designing specialized containers or scaled models.
3. The Sphere: Perfectly Symmetrical and Consistently Circular
The sphere, a perfectly symmetrical three-dimensional shape, is perhaps the most consistent producer of circular cross-sections among the geometric solids. It stands out due to its inherent spherical symmetry.
Understanding Spherical Cross-Sections
No matter how you slice a sphere, as long as the cut passes through the sphere's volume, you will always get a circular cross-section. This stems from its perfect radial symmetry.
-
Any Plane: Every plane that intersects the sphere's volume will create a circle. The diameter of this circle varies depending on the distance of the cutting plane from the sphere's center.
-
Great Circles: Planes passing through the sphere's center create the largest possible circles, known as "great circles." These great circles have a diameter equal to the sphere's diameter. The Earth's equator is a prime example of a great circle.
-
Smaller Circles: Planes that do not pass through the center yield smaller circles. The closer the plane is to the center, the larger the resulting circle. The further away, the smaller the circle until it eventually becomes a single point at the edge of the sphere.
Real-World Applications of Spheres
The consistent circular nature of spherical cross-sections leads to numerous applications:
-
Astronomy: Planets, stars, and moons are approximated as spheres. Their near-perfect spherical shape is the result of gravitational forces.
-
Sports: Balls in various sports (soccer, basketball, baseball) are spherical, with consistent circular cross-sections ensuring consistent flight and bounce characteristics.
-
Bearings: Spherical bearings allow for rotational freedom and minimal friction, a property directly linked to the consistent circular cross-sections.
-
Global Positioning: The spherical model of Earth is crucial for global navigation systems (GPS), mapping and navigation.
The predictable nature of spherical cross-sections makes spheres exceptionally important in design and engineering, where consistent features and precise measurements are crucial.
Conclusion: Circular Cross-Sections and Their Significance
The cylinder, cone, and sphere, each with its own unique characteristics, demonstrate the fascinating world of geometric solids and their cross-sections. While not every cross-section of a cone is circular, the consistent circular nature of the cylinder and the sphere, regardless of how they are sliced, makes them indispensable in various real-world applications. Understanding these properties is not only crucial for mathematical comprehension but also vital in numerous engineering, design, and scientific fields, showcasing the practical implications of geometric principles. The inherent geometric properties, particularly the consistent production of circular cross-sections, underpins their versatility and widespread usage across diverse disciplines. Furthermore, the study of these solids opens up an understanding of more complex geometric concepts and the importance of their cross-sectional analysis in problem-solving.
Latest Posts
Latest Posts
-
What Layer Isnt Continuoues And Tha Gaps Are Called
Apr 04, 2025
-
According To The Law Of Demand Other Things Being Equal
Apr 04, 2025
-
A Negatively Charged Particle In An Atom Is The
Apr 04, 2025
-
Common Passageway Of Food And Air
Apr 04, 2025
-
Which Equation Represents A Fission Reaction
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 3 Geometric Solids Which Have Circular Cross Sections . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
