25 4 As A Mixed Number
Juapaving
May 11, 2025 · 5 min read
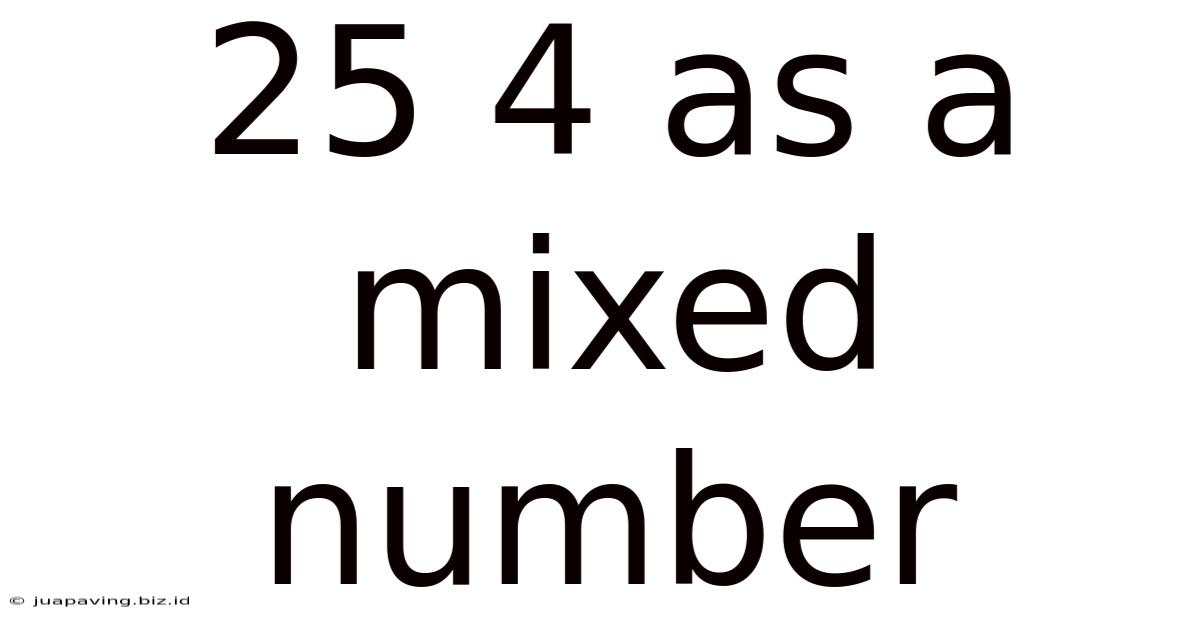
Table of Contents
25/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 25/4 into a mixed number, explaining the concepts involved and providing various methods for solving similar problems. We'll explore the underlying principles, practical applications, and offer helpful tips and tricks to master this essential mathematical operation.
Understanding Fractions and Mixed Numbers
Before we dive into the conversion of 25/4, let's review the basics. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 25/4, 7/3, 10/10). In contrast, a proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 2/5).
A mixed number combines a whole number and a proper fraction. It represents a quantity greater than one. For example, 2 1/2, 3 3/4, and 5 1/3 are all mixed numbers.
Converting 25/4 to a Mixed Number: The Division Method
The most common and straightforward method for converting an improper fraction like 25/4 into a mixed number is through division. Here's how it works:
- Divide the numerator by the denominator: Divide 25 by 4.
- Determine the whole number: The quotient (the result of the division) represents the whole number part of the mixed number. 25 divided by 4 is 6 with a remainder of 1. Therefore, our whole number is 6.
- Determine the fractional part: The remainder becomes the numerator of the fractional part of the mixed number. The denominator remains the same as the original fraction's denominator. Our remainder is 1, so the numerator of our fraction is 1. The denominator remains 4.
- Combine the whole number and the fraction: Combine the whole number from step 2 and the fraction from step 3 to form the mixed number. Therefore, 25/4 as a mixed number is 6 1/4.
Example Breakdown:
25 ÷ 4 = 6 with a remainder of 1
Whole number = 6
Numerator = 1 (remainder)
Denominator = 4
Mixed number = 6 1/4
Visualizing the Conversion: A Practical Approach
Imagine you have 25 quarters. Since four quarters make a dollar, you can group these 25 quarters into groups of four.
- Grouping: You can make six complete groups of four quarters each (6 * 4 = 24 quarters).
- Remainder: You'll have one quarter left over.
- Representation: This represents 6 whole dollars and 1/4 of a dollar. Therefore, 25/4 is equivalent to 6 1/4.
This visual approach helps to solidify the understanding of the concept, especially for those who benefit from concrete examples.
Alternative Methods: Understanding the Underlying Principles
While the division method is the most direct, other approaches reinforce the understanding of fraction manipulation:
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the denominator from the numerator until the result is less than the denominator.
- Subtract: Start by subtracting the denominator (4) from the numerator (25). 25 - 4 = 21.
- Repeat: Continue subtracting 4 until the result is less than 4. 21 - 4 = 17; 17 - 4 = 13; 13 - 4 = 9; 9 - 4 = 5; 5 - 4 = 1.
- Count the subtractions: You subtracted 4 six times. This is your whole number (6).
- Remaining fraction: The remaining value after repeated subtractions (1) becomes the numerator of your fraction. The denominator remains 4.
- Mixed number: Thus, you have 6 1/4.
Method 3: Using Equivalent Fractions (Less Practical for this specific example)
This method involves finding an equivalent fraction with a numerator that is a multiple of the denominator. While less efficient for this particular problem, understanding this principle is valuable for more complex fraction conversions. This method involves finding a common factor between the numerator and denominator and simplifying accordingly. For larger numbers, this method can become cumbersome.
Applications of Mixed Numbers
Understanding how to convert improper fractions to mixed numbers is crucial in various real-world applications and advanced mathematical concepts:
- Measurement: Expressing measurements (e.g., length, weight, volume) often involves mixed numbers. For instance, 6 1/4 inches is a more intuitive representation than 25/4 inches.
- Baking and Cooking: Recipes frequently use mixed numbers to specify ingredient quantities.
- Construction and Engineering: Accurate calculations in construction and engineering often require converting between improper fractions and mixed numbers for precise measurements.
- Time: Time is often expressed in mixed numbers (e.g., 2 1/2 hours).
Solving Similar Problems: Practicing Conversion
To solidify your understanding, let's practice converting a few more improper fractions to mixed numbers:
- 17/5: 17 divided by 5 is 3 with a remainder of 2. Therefore, 17/5 = 3 2/5.
- 23/6: 23 divided by 6 is 3 with a remainder of 5. Therefore, 23/6 = 3 5/6.
- 31/8: 31 divided by 8 is 3 with a remainder of 7. Therefore, 31/8 = 3 7/8.
By practicing these conversions, you'll become more comfortable and proficient in manipulating fractions and working with mixed numbers.
Simplifying Mixed Numbers
Once you've converted an improper fraction to a mixed number, remember to always simplify the fractional part if possible. For example, if you end up with a mixed number like 6 2/4, you would simplify the fraction 2/4 to 1/2, resulting in the simplified mixed number 6 1/2.
Conclusion: Mastering Fraction Conversions
Converting improper fractions to mixed numbers is a fundamental skill in mathematics with broad practical applications. Understanding the division method, along with the alternative methods, provides a solid foundation for handling various fractional calculations. By practicing regularly and visualizing the concepts, you can master this essential skill and confidently tackle more complex mathematical problems involving fractions. Remember, the key is to understand the underlying principles and choose the method that works best for you. Consistent practice and a solid grasp of the concepts will lead to fluency and confidence in handling fractions.
Latest Posts
Latest Posts
-
How Many Electrons Are In Na
May 11, 2025
-
Which Of The Following Is The Weakest Acid
May 11, 2025
-
What Is The Product Of A 5 And A 3
May 11, 2025
-
What Is The Potential Difference Between Points A And B
May 11, 2025
-
Is 1cc The Same As 1ml
May 11, 2025
Related Post
Thank you for visiting our website which covers about 25 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.