22.5 Is What Percent Of 90
Juapaving
May 12, 2025 · 4 min read
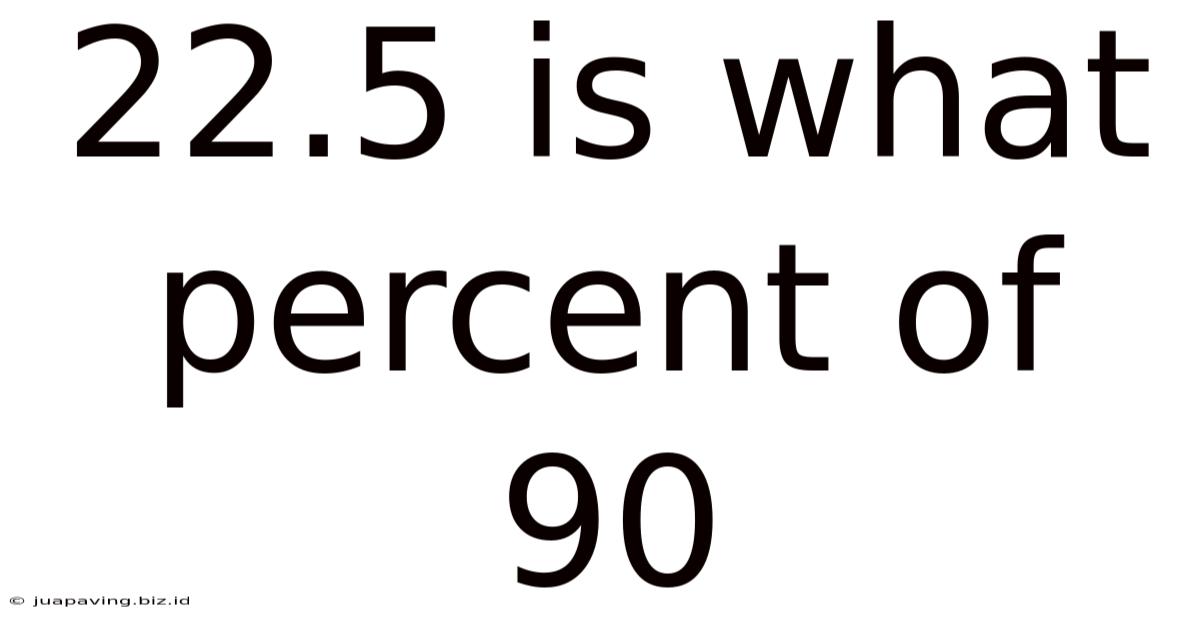
Table of Contents
22.5 is What Percent of 90: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and budgeting to data analysis and everyday life. This comprehensive guide will not only answer the question, "22.5 is what percent of 90?" but also delve into the underlying principles of percentage calculations, providing you with the tools and knowledge to tackle similar problems confidently. We’ll explore various methods, from basic arithmetic to utilizing formulas and even employing technology for efficient solutions.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The symbol used to represent percentage is "%". Essentially, it indicates how many parts of a whole exist, where the whole is divided into 100 equal parts. For example, 50% signifies 50 out of 100, or half.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 22.5 represents of 90 is by using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 22.5
- Whole: 90
Substituting these values into the formula:
(22.5 / 90) x 100 = Percentage
This simplifies to:
0.25 x 100 = 25%
Therefore, 22.5 is 25% of 90.
Method 2: Simplifying the Fraction
Before applying the formula, we can simplify the fraction (22.5 / 90) to make the calculation easier. Notice that both numbers are divisible by 22.5:
22.5 / 90 = 1/4
Now, converting the fraction 1/4 to a percentage:
(1/4) x 100 = 25%
This confirms our previous result: 22.5 is 25% of 90.
Method 3: Using Proportions
Another approach involves setting up a proportion:
x/100 = 22.5/90
To solve for 'x' (the percentage), cross-multiply:
90x = 22.5 * 100
90x = 2250
x = 2250 / 90
x = 25
Therefore, x = 25%. This method demonstrates the relationship between the parts and the whole in a proportional manner.
Method 4: Utilizing Decimal Conversion
We can convert the fraction 22.5/90 into a decimal first, then multiply by 100 to obtain the percentage.
22.5 / 90 = 0.25
0.25 x 100 = 25%
Expanding on Percentage Calculations: Different Scenarios
While the above methods effectively solve "22.5 is what percent of 90?", understanding percentage calculations extends far beyond this single problem. Let's explore some related scenarios:
Scenario 1: Finding the Whole
What if we knew the percentage and the part, but needed to find the whole? For example:
15% of what number is 30?
We can adapt the formula:
(Part / Percentage) x 100 = Whole
(30 / 15) x 100 = 200
Therefore, 15% of 200 is 30.
Scenario 2: Finding the Part
Suppose we know the percentage and the whole, and need to find the part. For instance:
What is 40% of 80?
We modify the formula to:
(Percentage / 100) x Whole = Part
(40 / 100) x 80 = 32
Therefore, 40% of 80 is 32.
Scenario 3: Percentage Increase/Decrease
Percentage calculations are crucial in understanding increases and decreases. For example, if a price increases from $50 to $60, the percentage increase is calculated as follows:
((New Value - Old Value) / Old Value) x 100 = Percentage Increase
((60 - 50) / 50) x 100 = 20%
Similarly, a decrease can be calculated using the same formula.
Practical Applications of Percentage Calculations
The applications of percentage calculations are vast and diverse. Here are some examples:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Data Analysis: Representing data proportions, trends, and changes in statistical reports.
- Sales and Marketing: Determining conversion rates, customer acquisition costs, and market share.
- Everyday Life: Calculating tips, sales tax, discounts at stores, and understanding proportions in recipes.
Advanced Techniques and Tools
For more complex percentage calculations, or when dealing with large datasets, advanced techniques and tools can greatly enhance efficiency:
- Spreadsheets (Excel, Google Sheets): Spreadsheets offer built-in functions like
PERCENTAGE, which simplifies percentage calculations and allows for bulk calculations. - Programming Languages (Python, R): These languages provide libraries and functions designed for numerical computations, enabling automation and sophisticated analyses.
- Online Calculators: Numerous online percentage calculators are readily available, offering convenient and quick solutions.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with broad applicability. By understanding the fundamental concepts and various methods – from basic arithmetic to utilizing formulas and leveraging technology – you can confidently tackle various percentage-related problems. Remember the core formula: (Part / Whole) x 100 = Percentage, and adapt it based on what you need to find. With practice and understanding, you’ll become proficient in this essential mathematical skill, improving your problem-solving capabilities across multiple disciplines. This comprehensive guide provides a solid foundation for navigating the world of percentages with ease and accuracy. Remember to practice regularly to reinforce your learning and build confidence in your abilities.
Latest Posts
Latest Posts
-
What Type Of Mirror Is Being Used In The Image
May 12, 2025
-
Which Of The Following Is Not A Business Transaction
May 12, 2025
-
Who Is The Father Of Humanism
May 12, 2025
-
A Group Of Cows Are Called
May 12, 2025
-
What Is The Lowest Common Multiple Of 6 And 21
May 12, 2025
Related Post
Thank you for visiting our website which covers about 22.5 Is What Percent Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.