2 3/4 As An Improper Fraction
Juapaving
Apr 08, 2025 · 5 min read
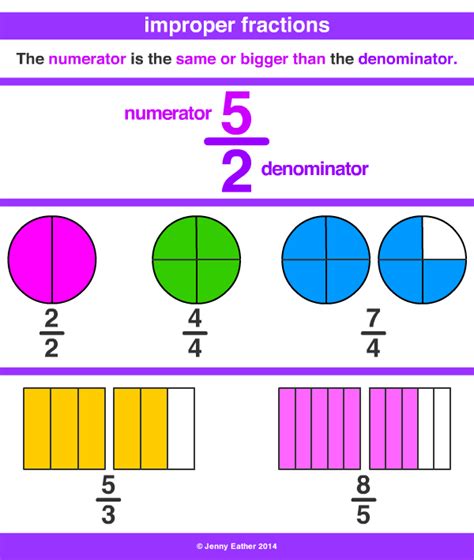
Table of Contents
2 3/4 as an Improper Fraction: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, forming the building blocks for more complex concepts. Mixed numbers, like 2 3/4, and improper fractions are two ways of representing the same value. While mixed numbers clearly show a whole number part and a fractional part, improper fractions express the value as a single fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). This article will delve deeply into converting the mixed number 2 3/4 into an improper fraction, explaining the process, providing examples, and exploring the broader significance of this conversion in various mathematical applications.
Understanding Mixed Numbers and Improper Fractions
Before diving into the conversion, let's solidify our understanding of the two fraction types:
Mixed Numbers: These combine a whole number and a proper fraction. A proper fraction is one where the numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8). The mixed number 2 3/4 represents two whole units and three-quarters of another unit.
Improper Fractions: In an improper fraction, the numerator is greater than or equal to the denominator (e.g., 5/4, 7/3, 8/8). This indicates a value greater than or equal to one whole unit. While they might seem less intuitive than mixed numbers at first glance, improper fractions are incredibly useful in mathematical operations, especially when adding, subtracting, multiplying, and dividing fractions.
Converting 2 3/4 to an Improper Fraction: The Step-by-Step Process
The conversion of 2 3/4 to an improper fraction involves a straightforward two-step process:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 2, and the denominator is 4. Therefore, we multiply 2 * 4 = 8.
Step 2: Add the numerator to the result from Step 1.
The numerator is 3. Adding this to the result from Step 1 (8), we get 8 + 3 = 11.
Step 3: Keep the same denominator.
The denominator remains unchanged throughout the conversion. Therefore, the denominator stays as 4.
Result: Combining the results from Steps 2 and 3, we get the improper fraction 11/4. This means that 2 3/4 is equivalent to 11/4.
Visualizing the Conversion
Imagine you have two whole pizzas and three-quarters of a third pizza. To represent this as an improper fraction, we need to express the total number of pizza slices in terms of quarter-slices (since the denominator is 4).
Each whole pizza has 4 quarter-slices. Two whole pizzas therefore have 2 * 4 = 8 quarter-slices. Adding the three additional quarter-slices from the third pizza, we have a total of 8 + 3 = 11 quarter-slices. Since each slice is a quarter, the total is represented as 11/4.
Practical Applications of Improper Fractions
Improper fractions are essential in various mathematical contexts:
-
Simplifying Calculations: Adding and subtracting fractions becomes much easier when all fractions are in improper form. Having a common denominator is crucial for these operations, and improper fractions often facilitate finding this common denominator more easily.
-
Algebra: In algebraic expressions and equations involving fractions, improper fractions are frequently used to simplify calculations and solve for unknown variables. The elegance and efficiency of working with improper fractions often simplify complex algebraic manipulations.
-
Calculus: Improper fractions are integral (pun intended!) to calculus, especially when dealing with derivatives and integrals that involve rational functions (fractions with polynomials in the numerator and denominator).
-
Geometry and Measurement: In geometrical problems involving area, volume, or measurement, improper fractions might represent portions of shapes or quantities exceeding a whole unit.
-
Real-World Applications: Many real-world scenarios, from baking (measuring ingredients) to construction (measuring materials), benefit from using improper fractions for precise calculations.
Further Examples of Converting Mixed Numbers to Improper Fractions
Let's solidify our understanding with a few more examples:
-
3 1/2: (3 * 2) + 1 = 7. The improper fraction is 7/2.
-
1 2/3: (1 * 3) + 2 = 5. The improper fraction is 5/3.
-
5 3/8: (5 * 8) + 3 = 43. The improper fraction is 43/8.
-
10 1/4: (10 * 4) + 1 = 41. The improper fraction is 41/4.
-
7 5/6: (7 * 6) + 5 = 47. The improper fraction is 47/6.
These examples demonstrate the consistent application of the two-step process: multiply the whole number by the denominator and add the numerator, keeping the original denominator.
Converting Improper Fractions Back to Mixed Numbers
The process is easily reversible. To convert an improper fraction back to a mixed number:
- Divide the numerator by the denominator. The quotient is the whole number part of the mixed number.
- The remainder becomes the numerator of the proper fraction.
- Keep the original denominator.
For example, to convert 11/4 back to a mixed number:
- 11 ÷ 4 = 2 with a remainder of 3.
- The remainder is 3.
- The denominator remains 4.
Therefore, 11/4 = 2 3/4.
Conclusion: Mastering Fraction Conversions
The ability to convert between mixed numbers and improper fractions is a crucial skill in mathematics. Understanding the conversion process not only improves computational efficiency but also enhances problem-solving capabilities across numerous mathematical fields and real-world applications. By mastering this seemingly simple conversion, you build a stronger foundation for more advanced mathematical concepts and applications. Remember the core steps: multiply, add, and keep the denominator! This empowers you to approach a wide range of problems with confidence and precision. The ability to seamlessly switch between mixed numbers and improper fractions is a mark of mathematical fluency and a significant step toward mathematical mastery.
Latest Posts
Latest Posts
-
Functional Group With A Face Funny
Apr 08, 2025
-
What Do You Call A Group Of Lions
Apr 08, 2025
-
Whats The Lcm Of 9 And 12
Apr 08, 2025
-
Which Is Not One Of The Five Pillars Of Islam
Apr 08, 2025
-
How Many Feet Is 65 In
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about 2 3/4 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.