2 1 2 As A Percent
Juapaving
Apr 08, 2025 · 5 min read
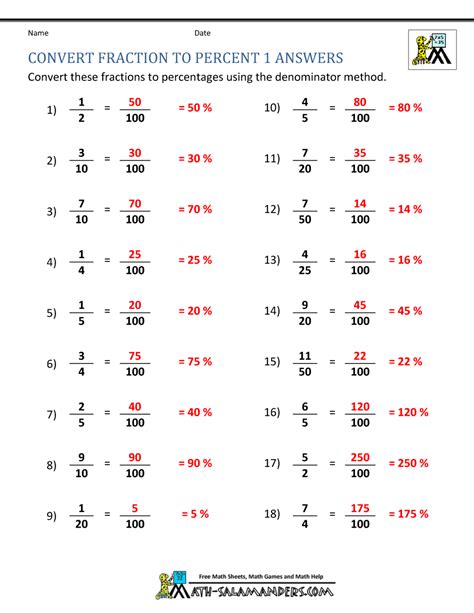
Table of Contents
2/12 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 2/12 into a percentage, exploring different methods and providing a deeper understanding of the underlying concepts. We will also explore related concepts and provide examples to solidify your understanding.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, the fraction is 2/12, where 2 is the numerator and 12 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, or 50/100.
Method 1: Simplifying the Fraction First
The fraction 2/12 can be simplified before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD of 2 and 12 is 2.
-
Divide both the numerator and the denominator by their GCD: 2 ÷ 2 = 1 12 ÷ 2 = 6
-
The simplified fraction is: 1/6
Now, we can convert the simplified fraction 1/6 to a percentage.
Method 2: Converting the Simplified Fraction to a Percentage
There are two primary ways to convert a fraction to a percentage:
A. Using Division:
-
Divide the numerator by the denominator: 1 ÷ 6 ≈ 0.1667
-
Multiply the result by 100: 0.1667 × 100 = 16.67%
Therefore, 1/6 (and consequently, 2/12) is approximately 16.67%.
B. Using Equivalent Fractions:
To convert a fraction to a percentage directly, you need to create an equivalent fraction with a denominator of 100. However, this method isn't always straightforward, especially with fractions that don't easily convert to a denominator of 100. In this case, the method of division is more efficient.
While an equivalent fraction with a denominator of 100 isn't easily attainable for 1/6, understanding this method is crucial for fractions that can be easily converted. For instance, 1/4 can be easily converted to 25/100 (by multiplying both numerator and denominator by 25) which is equivalent to 25%.
Method 3: Converting the Original Fraction Directly
While simplifying is generally recommended, let's demonstrate converting the original fraction 2/12 directly to a percentage using the division method.
-
Divide the numerator by the denominator: 2 ÷ 12 ≈ 0.1667
-
Multiply the result by 100: 0.1667 × 100 = 16.67%
This confirms that both methods yield the same result: 2/12 is approximately 16.67%.
Understanding the Decimal Value
The decimal value obtained during the conversion process (0.1667 in this case) represents the fraction as a decimal. This decimal is crucial in various calculations and is often the intermediate step before expressing the fraction as a percentage.
Rounding and Precision
The percentage value 16.67% is a rounded value. The actual decimal representation of 1/6 is a repeating decimal (0.166666...). The degree of rounding depends on the desired level of precision. For most practical purposes, two decimal places (16.67%) are sufficient.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is invaluable in various real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins.
- Statistics: Representing data and probabilities.
- Everyday Life: Understanding sales, tip calculations, and survey results.
Further Exploration: Similar Fraction Conversions
Let's consider a few more examples to solidify our understanding:
- 1/3 as a percentage: 1 ÷ 3 ≈ 0.3333; 0.3333 × 100 ≈ 33.33%
- 3/4 as a percentage: 3 ÷ 4 = 0.75; 0.75 × 100 = 75%
- 5/8 as a percentage: 5 ÷ 8 = 0.625; 0.625 × 100 = 62.5%
These examples highlight the versatility of the conversion method and its application across different fractions.
Advanced Concepts: Working with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To convert a mixed number to a percentage, first convert it to an improper fraction, and then follow the same conversion steps outlined above.
For example, to convert 1 1/2 to a percentage:
-
Convert to an improper fraction: 1 1/2 = (1 × 2 + 1) / 2 = 3/2
-
Divide the numerator by the denominator: 3 ÷ 2 = 1.5
-
Multiply by 100: 1.5 × 100 = 150%
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions like 2/12 to percentages is a straightforward process involving division and multiplication. Understanding the underlying principles of fractions and percentages, along with mastering the different conversion methods, empowers you to confidently tackle various mathematical and real-world problems involving fractions and percentages. Remember to simplify fractions whenever possible to ease the calculation process and enhance accuracy. The skill of converting fractions to percentages is an invaluable asset across various disciplines and everyday life scenarios. Through consistent practice and application, you can effortlessly master this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Which Of The Following Is An Electrolyte
Apr 08, 2025
-
Lowest Common Multiple Of 3 And 10
Apr 08, 2025
-
Why Is Pure Acetic Acid Often Called Glacial Acetic Acid
Apr 08, 2025
-
Whats The Difference Between Women And Woman
Apr 08, 2025
-
What Is 102 Fahrenheit In Celsius
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about 2 1 2 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.