15 Decreased By Twice A Number
Juapaving
May 13, 2025 · 5 min read
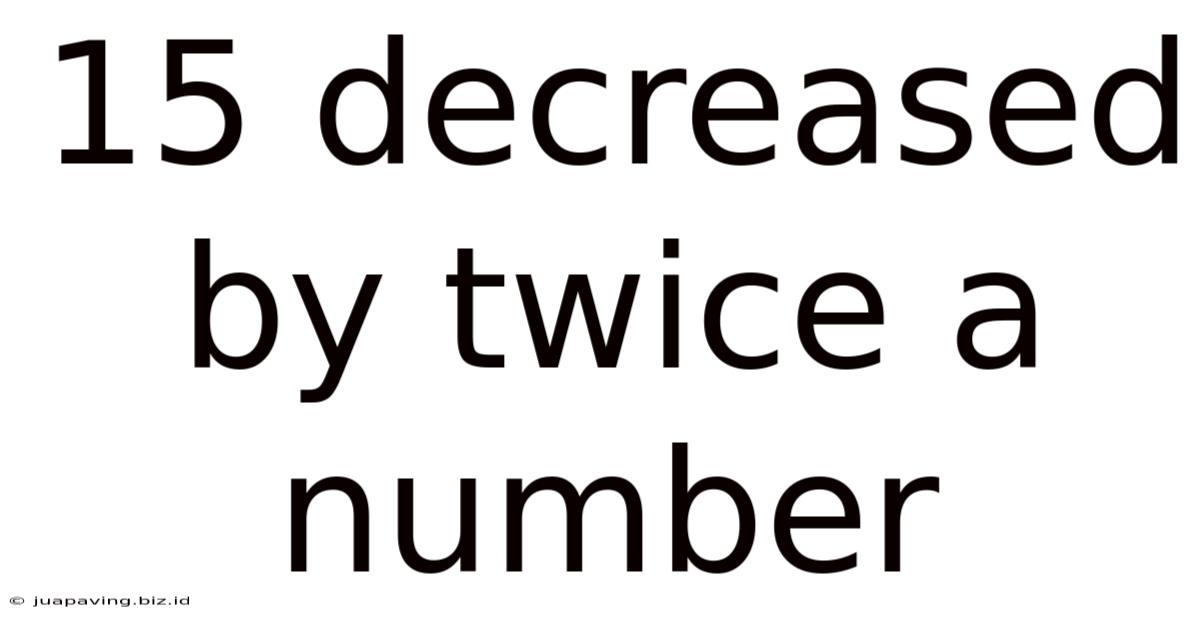
Table of Contents
15 Decreased by Twice a Number: A Comprehensive Exploration
This article delves into the mathematical expression "15 decreased by twice a number," exploring its various interpretations, applications, and solutions. We'll unpack the meaning, translate it into algebraic equations, solve for different scenarios, and discuss its relevance in real-world problems. The focus will be on understanding the underlying concepts and building a strong foundation in algebraic thinking.
Understanding the Expression: "15 Decreased by Twice a Number"
The phrase "15 decreased by twice a number" represents a mathematical operation. Let's break it down:
- 15: This is a constant value.
- Decreased by: This indicates subtraction.
- Twice a number: This means two times an unknown number. We typically represent an unknown number with a variable, such as 'x' or 'n'.
Therefore, the phrase translates to: 15 - 2n (where 'n' represents the unknown number).
Translating into Algebraic Equations
The core of solving mathematical word problems lies in translating the given information into algebraic equations. In this case, the phrase "15 decreased by twice a number" directly translates to the algebraic expression:
15 - 2n
This simple expression forms the basis for various mathematical problems. The complexity arises when this expression is part of a larger equation or inequality, where we need to solve for the unknown variable 'n'.
Solving for 'n' in Different Scenarios
The simplest scenario is when the expression "15 - 2n" is equated to a specific value. Let's explore a few examples:
Scenario 1: 15 - 2n = 7
To solve for 'n', we follow these steps:
- Subtract 15 from both sides: -2n = 7 - 15 => -2n = -8
- Divide both sides by -2: n = -8 / -2 => n = 4
Therefore, if "15 decreased by twice a number" equals 7, then the number is 4.
Scenario 2: 15 - 2n = 0
- Subtract 15 from both sides: -2n = -15
- Divide both sides by -2: n = -15 / -2 => n = 7.5
In this case, if the expression equals zero, the number is 7.5.
Scenario 3: 15 - 2n > 5 (Inequality)
This scenario introduces an inequality. The solution involves finding the range of values for 'n' that satisfy the inequality:
- Subtract 15 from both sides: -2n > 5 - 15 => -2n > -10
- Divide both sides by -2 (remember to reverse the inequality sign when dividing by a negative number): n < 5
This means that any number less than 5 will satisfy the inequality "15 decreased by twice a number is greater than 5."
Scenario 4: 15 - 2n ≤ 11
- Subtract 15 from both sides: -2n ≤ 11 - 15 => -2n ≤ -4
- Divide both sides by -2 (reverse the inequality sign): n ≥ 2
This inequality is satisfied by any number greater than or equal to 2.
Real-World Applications
The expression "15 decreased by twice a number" might seem abstract, but it finds applications in various real-world situations. Consider these examples:
-
Profit Calculation: Imagine a business with a starting profit of $15. If they lose $2 for every unit of a product they sell, the expression 15 - 2n represents their profit after selling 'n' units. Setting this equal to zero helps find the break-even point.
-
Temperature Change: Suppose the temperature is 15°C, and it decreases by 2°C every hour. The expression 15 - 2n represents the temperature after 'n' hours. Setting this equal to a specific temperature helps determine the time it takes to reach that temperature.
-
Inventory Management: A warehouse has 15 units of a particular item. If they sell two units each day, the expression 15 - 2n represents the remaining inventory after 'n' days. Setting this to zero indicates when the inventory runs out.
Graphical Representation
The expression 15 - 2n can be effectively visualized using a graph. Plotting this linear equation (y = 15 - 2x) reveals its slope and y-intercept. The y-intercept is 15, indicating the starting value. The slope is -2, demonstrating a decrease of 2 units for every unit increase in x. This graphical representation provides an intuitive understanding of how the value changes with different values of 'n'.
Extending the Concept: More Complex Scenarios
The basic expression can be integrated into more complex equations and problems. For instance, you might encounter scenarios like:
- (15 - 2n) + 5 = 12 (Here, you would first simplify the equation to 20 - 2n = 12 and then solve for 'n').
- (15 - 2n)² = 25 (This involves solving a quadratic equation).
- Word problems incorporating the expression into a larger narrative, requiring careful translation into an equation before solving.
These more complex scenarios demand a more thorough understanding of algebraic manipulation and equation-solving techniques, including quadratic equations and systems of equations.
Developing Strong Algebraic Skills
Mastering the concept of "15 decreased by twice a number" is crucial for building a solid foundation in algebra. Consistent practice with various problems, involving different scenarios and levels of complexity, is key to strengthening your algebraic skills. Start with simple equations and gradually progress to more challenging problems, including those involving inequalities and quadratic equations.
Remember to break down each problem systematically, translating the word problem into an algebraic equation, and applying appropriate solving techniques. Regular practice and a systematic approach will significantly improve your ability to confidently tackle algebraic problems.
Conclusion: Beyond the Numbers
The seemingly simple expression, "15 decreased by twice a number," provides a fertile ground for exploring fundamental algebraic concepts. From simple equation solving to more complex scenarios involving inequalities and quadratic equations, this expression offers a stepping stone to a deeper understanding of mathematics and its application in solving real-world problems. By mastering this concept and continuously practicing different problem types, you can build a strong foundation in algebraic thinking, essential for success in higher-level mathematics and STEM fields. The key lies in diligent practice, careful analysis, and a systematic approach to problem-solving. The understanding gained from this simple expression will serve as a building block for more complex mathematical explorations.
Latest Posts
Latest Posts
-
7 Characteristics Of Pea Plants By Gregor Mendel
May 13, 2025
-
What Is The Greatest Common Factor Of 6 And 10
May 13, 2025
-
Plot Rational Numbers On A Number Line
May 13, 2025
-
6 9 Rounded To The Nearest Tenth
May 13, 2025
-
What Is The Difference Between Chemical Reaction And Nuclear Reaction
May 13, 2025
Related Post
Thank you for visiting our website which covers about 15 Decreased By Twice A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.