1 X 1 X 2 1 X 3
Juapaving
May 14, 2025 · 6 min read
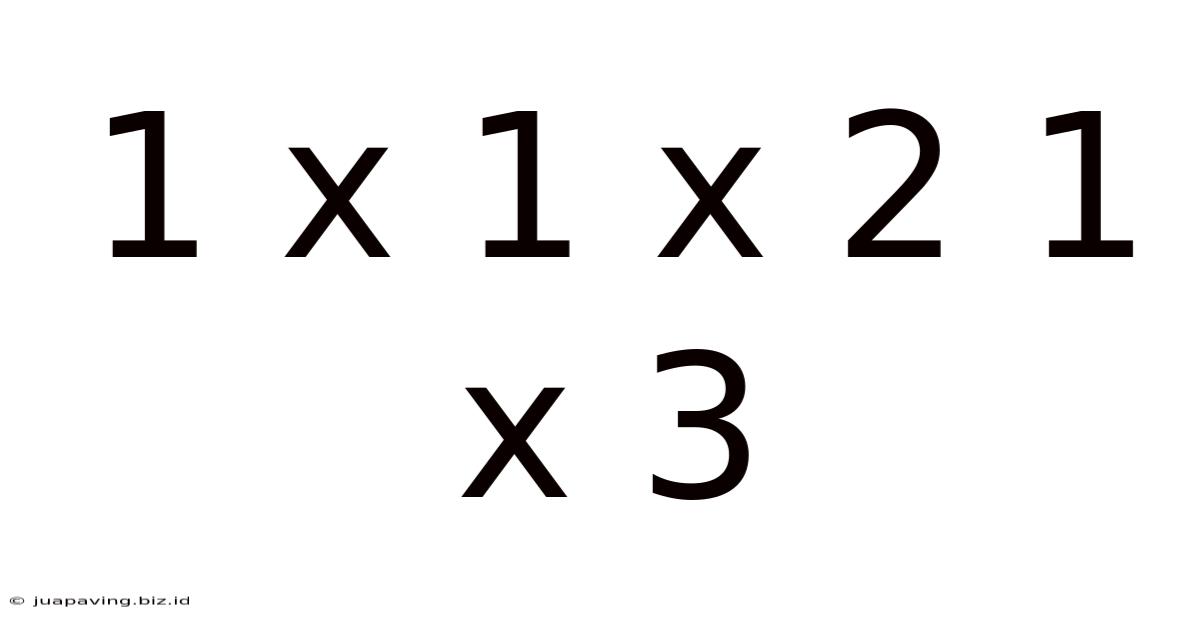
Table of Contents
Decoding the Enigma: A Deep Dive into 1 x 1 x 2 & 1 x 3
The seemingly simple numerical expressions "1 x 1 x 2" and "1 x 3" might initially appear trivial. However, a closer examination reveals a surprising depth, opening doors to mathematical concepts, practical applications, and even philosophical interpretations. This exploration delves into the multifaceted nature of these expressions, examining their inherent properties, exploring their extensions, and considering their relevance across various disciplines.
The Basics: Multiplication and its Implications
At their core, "1 x 1 x 2" and "1 x 3" represent basic multiplication operations. Multiplication, a fundamental arithmetic operation, signifies repeated addition. In "1 x 1 x 2," we're essentially adding one to itself zero times (1 x 1 = 1), then adding that result to itself twice (1 x 2 = 2). Similarly, "1 x 3" involves adding one to itself three times (1 + 1 + 1 = 3). While the answers are straightforward (2 and 3 respectively), the underlying principles are far-reaching.
Understanding the Identity Property of Multiplication: The presence of '1' in both expressions highlights the identity property of multiplication. This property states that any number multiplied by 1 remains unchanged. This seemingly simple concept is crucial in various mathematical operations, from simplifying complex equations to scaling variables in scientific models. The identity property ensures consistency and allows for easier manipulation within mathematical frameworks.
Extending the Concept: Beyond Simple Multiplication
While the initial expressions are simple, we can expand their scope by considering various extensions and interpretations. For instance:
-
Higher Dimensions: Imagine extending "1 x 1 x 2" to represent the volume of a rectangular prism. In this context, 1 could represent the length and width, and 2 could represent the height. This illustrates the application of basic multiplication in three-dimensional geometry. Similar spatial interpretations could be applied to more complex scenarios, modeling real-world objects and spaces.
-
Sequential Operations: The expressions can be interpreted as sequential operations. For example, "1 x 1 x 2" could represent a process where an initial value (1) undergoes a transformation (multiplied by 1, resulting in no change), followed by another transformation (multiplied by 2, doubling the value). This sequential process can model various systems, from population growth to financial investments, where a value changes through multiple stages.
-
Abstract Algebra: In abstract algebra, the concept of multiplication takes on a more generalized form. The expressions "1 x 1 x 2" and "1 x 3" can be viewed within the context of groups and rings, where the numbers are elements within a defined algebraic structure. This abstract perspective provides a deeper understanding of mathematical operations and their underlying symmetries.
Practical Applications: Where the Numbers Matter
The seemingly trivial expressions "1 x 1 x 2" and "1 x 3" find surprising applications in various fields:
-
Computer Science: Binary arithmetic, the foundation of computer operations, relies heavily on the manipulation of 1s and 0s. Though not directly equivalent, these expressions provide a basic understanding of numerical manipulation that's essential in coding and programming. Calculations in binary often involve the repeated multiplication and addition of 1s and 0s, mirroring the underlying principles of these simple expressions.
-
Physics: Simple scaling and proportionality often involve multiplication by a constant factor. Think of Newton's second law of motion (F = ma): if the mass (m) is 1 and the acceleration (a) is 3, the force (F) is simply 1 x 3 = 3 units of force. The expressions provide a foundational understanding for more complex physical calculations.
-
Engineering: Scaling designs, calculating material quantities, and determining structural loads often necessitate fundamental multiplication operations. These simple expressions lay the groundwork for more sophisticated engineering calculations. Imagine scaling a blueprint: if a dimension is 1 unit and it needs to be tripled, the calculation is directly analogous to 1 x 3.
-
Economics & Finance: Simple interest calculations often involve multiplying the principal amount by the interest rate. While practical financial calculations are often much more complex, the core principle remains rooted in multiplication. The conceptual understanding derived from "1 x 3" extends to understanding the effects of compounded interest over time.
The Philosophical Underpinnings: Exploring Deeper Meanings
Beyond the practical applications, these simple expressions invite philosophical contemplation:
-
The Nature of Numbers: The expressions prompt reflection on the fundamental nature of numbers themselves. What does it mean for a number to be multiplied? How do numbers interact with each other? These questions engage with fundamental aspects of mathematics and its relationship to reality.
-
Simplicity and Complexity: The stark simplicity of "1 x 1 x 2" and "1 x 3" contrasts sharply with the complexity that emerges when dealing with more intricate mathematical operations. This contrast highlights the profound impact of small changes and the potential for escalating complexity.
-
The Power of Multiplication: Multiplication is a transformative operation. It allows us to scale, amplify, and exponentially expand upon initial values. The simple act of multiplying by 3 highlights the power of multiplicative growth, evident in various aspects of life, from population growth to technological advancement.
Expanding the Scope: Connecting to Broader Mathematical Concepts
The simplicity of "1 x 1 x 2" and "1 x 3" allows us to connect them to broader mathematical concepts:
-
Factorials: While not directly related, the concept of factorials (e.g., 3! = 3 x 2 x 1) involves repeated multiplication, echoing the principles present in "1 x 1 x 2." Understanding these simple multiplications aids in grasping the more complex concept of factorials and their implications in combinatorics and probability.
-
Series and Sequences: These simple expressions can be viewed as the initial terms in a sequence. For example, "1 x 3" could be part of a sequence such as 1 x 3, 2 x 3, 3 x 3, and so on. This opens up a broader understanding of mathematical patterns and their progression.
-
Exponents and Powers: Repeated multiplication leads to exponents. "1 x 1 x 2" could be interpreted as 1 raised to the power of 1, multiplied by 2 (1¹ x 2). This connection helps to establish a bridge between basic multiplication and the more advanced concept of exponentiation.
Conclusion: The Enduring Significance of Simple Arithmetic
In conclusion, while the expressions "1 x 1 x 2" and "1 x 3" seem elementary, their significance extends far beyond their immediate numerical values. They serve as fundamental building blocks for more advanced mathematical concepts, find practical applications in various fields, and even invite philosophical reflection on the nature of numbers and their operations. Their simplicity masks a depth of meaning that underscores the power and beauty of mathematical principles in shaping our understanding of the world around us. By exploring these seemingly insignificant expressions, we gain a deeper appreciation for the interconnectedness of mathematical ideas and their crucial role in shaping our understanding of the universe. The seemingly trivial becomes profound when examined with curiosity and attention to detail, proving that even the simplest concepts can hold immense potential for learning and discovery.
Latest Posts
Latest Posts
-
What Is The Difference Between A Pyramid And Prism
May 14, 2025
-
Molar Mass Of Oxalic Acid Dihydrate
May 14, 2025
-
Letter For Authorization To Collect Documents
May 14, 2025
-
How Many Feet In 25 Inches
May 14, 2025
-
5 3 And A Half In Cm
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 X 2 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.