1 X 1 2 X 2 4 X 4
Juapaving
May 14, 2025 · 6 min read
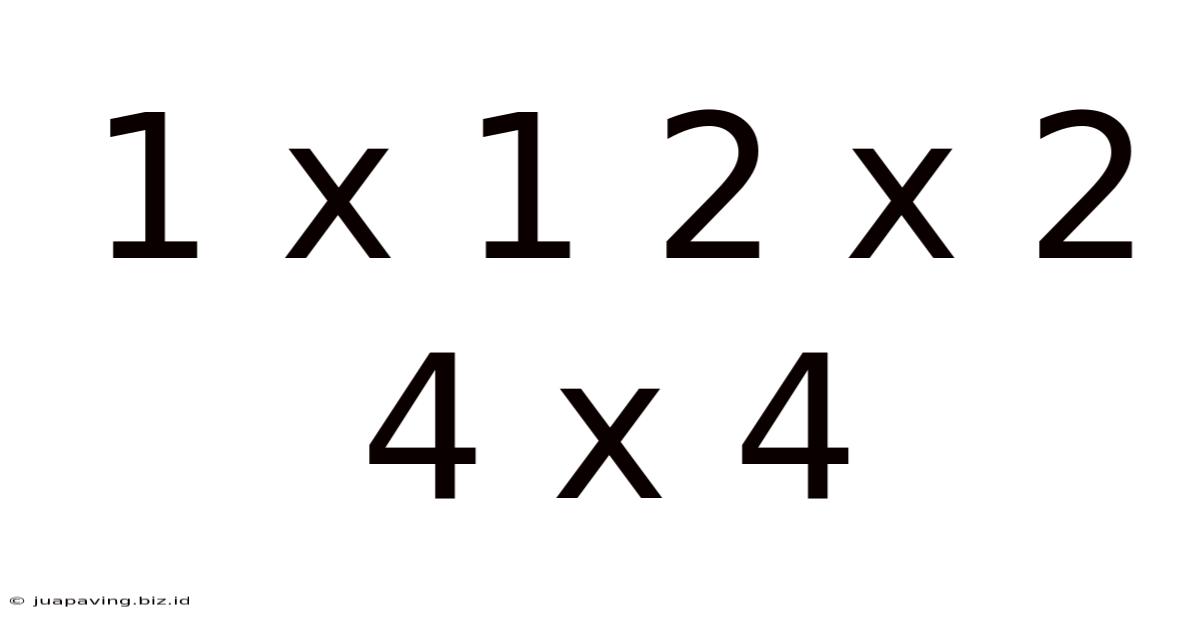
Table of Contents
Decoding the Patterns: Exploring the Mathematical and Algorithmic Implications of 1x1, 2x2, and 4x4 Matrices
The seemingly simple sequences "1x1," "2x2," and "4x4" conceal a wealth of mathematical concepts and computational implications, particularly within the realm of linear algebra and computer science. This exploration delves into the properties, applications, and underlying principles of these matrix dimensions, revealing their significance in diverse fields.
Understanding Matrices: The Foundation
Before delving into the specifics of 1x1, 2x2, and 4x4 matrices, it's crucial to establish a foundational understanding of matrices themselves. A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. The dimensions of a matrix are defined by the number of rows and columns it contains; thus, an m x n matrix has m rows and n columns. These dimensions are fundamental in determining the matrix's properties and the operations that can be performed on it.
1x1 Matrices: The Simplest Case
A 1x1 matrix is the most basic form, consisting of a single element. While seemingly trivial, it still adheres to the fundamental rules of matrix algebra. For instance, addition and multiplication with other 1x1 matrices (or scalars) follow standard arithmetic rules. Consider the 1x1 matrix [a]. Adding another 1x1 matrix [b] results in [a + b], and multiplying it by a scalar k yields [ka]. Though simple, this forms the foundation for understanding more complex matrix operations. Its significance lies in its role as a building block for larger matrices and its representation of a single scalar value within a matrix framework.
Example:
[5] + [3] = [8]
2 * [5] = [10]
2x2 Matrices: A Stepping Stone to Complexity
2x2 matrices represent a significant step up in complexity. They contain four elements arranged in two rows and two columns. These matrices are extensively used in various applications, including:
-
Transformations in 2D Graphics: Rotation, scaling, and shearing of images or shapes can be elegantly represented and computed using 2x2 matrices. This makes them fundamental in computer graphics, game development, and image processing.
-
Linear Systems of Equations: Systems of two linear equations with two unknowns can be compactly represented and solved using 2x2 matrices and their associated techniques, like finding determinants and inverses.
-
Representing Linear Transformations: A 2x2 matrix can represent a linear transformation in a two-dimensional space, mapping vectors from one point to another in a linear fashion.
Properties of 2x2 Matrices:
-
Determinant: The determinant of a 2x2 matrix
[[a, b], [c, d]]is calculated asad - bc. The determinant reveals crucial information about the matrix, including its invertibility (whether an inverse matrix exists). A non-zero determinant signifies an invertible matrix. -
Inverse: The inverse of a 2x2 matrix exists only if its determinant is non-zero. The inverse is used in solving systems of equations and performing inverse transformations.
-
Eigenvalues and Eigenvectors: These represent intrinsic properties of the linear transformation described by the 2x2 matrix. They are critical in various applications, including principal component analysis and stability analysis of systems.
Example:
Let's consider the matrix A = [[2, 1], [1, 2]].
- Determinant: (2 * 2) - (1 * 1) = 3
- Inverse: (1/3) *
[[2, -1], [-1, 2]]
4x4 Matrices: Power and Applications in 3D and Beyond
4x4 matrices become essential when dealing with three-dimensional space and beyond. Their extensive use stems from their capability to:
-
Represent 3D Transformations: They are fundamental in 3D computer graphics, allowing for efficient representation and computation of transformations like rotations, translations, scaling, and shearing in three-dimensional space. This is crucial for rendering 3D models, animations, and virtual reality environments.
-
Perspective Projections: 4x4 matrices are crucial in projecting 3D scenes onto a 2D screen, accounting for perspective effects. This is a cornerstone of realistic 3D rendering.
-
Homogeneous Coordinates: The use of a fourth coordinate in a 4x4 matrix allows for the concise representation of both linear and affine transformations (those involving translation) within a single matrix multiplication. This simplifies computations and reduces the need for separate transformation steps.
-
Computer Vision and Robotics: 4x4 matrices play a critical role in computer vision algorithms for object recognition and tracking, as well as in robotics for robot arm control and positioning.
Properties of 4x4 Matrices:
The properties of 4x4 matrices extend the concepts observed in 2x2 matrices, although calculations become significantly more involved. Determinants, inverses, eigenvalues, and eigenvectors are still relevant, but their computation requires more complex algorithms. The increased dimensionality adds layers of complexity to matrix operations and analysis.
Example: A 4x4 transformation matrix might represent a combination of rotation around the X-axis, translation along the Z-axis, and scaling along the Y-axis, all within a single matrix. Multiplying a 4D vector representing a point in space by this matrix yields the transformed point's coordinates.
Algorithmic Implications and Computational Efficiency
The size of a matrix directly impacts the computational resources required for various operations. As matrix dimensions increase, the number of calculations required grows rapidly. This has significant implications for the efficiency of algorithms that utilize matrices.
Computational Complexity: A Growing Concern
Algorithms operating on matrices often have computational complexity that scales with the square or cube of the matrix's dimensions (O(n²) or O(n³), where n is the dimension). This means that doubling the matrix size can significantly increase the computation time. For large matrices, optimizing algorithms and utilizing efficient data structures becomes critical to ensure feasible processing times.
Optimization Techniques for Matrix Operations
Various techniques aim to enhance the efficiency of matrix operations:
-
Strassen's Algorithm: This algorithm provides a faster method for matrix multiplication than the standard approach, particularly for larger matrices.
-
Parallel Computing: Distributing the matrix operations across multiple processors can significantly reduce the overall computation time, making it feasible to process large matrices within reasonable timeframes.
-
Sparse Matrix Representations: For matrices containing many zero elements (sparse matrices), specialized data structures can drastically reduce memory consumption and improve the efficiency of operations.
Real-World Applications: A Broad Spectrum
The applications of 1x1, 2x2, and 4x4 matrices are vast and span various disciplines:
-
Computer Graphics and Game Development: As previously mentioned, these matrices are integral to rendering 3D scenes, creating realistic animations, and enabling interactive game environments.
-
Physics Simulations: Matrices are used to represent and solve equations governing physical systems, ranging from simple spring-mass systems to complex fluid dynamics simulations.
-
Machine Learning: Matrices are fundamental to machine learning algorithms, particularly in representing data, performing linear regressions, and training neural networks. Matrix operations are the backbone of many machine learning techniques.
-
Signal Processing: Matrices are used to represent and manipulate signals, enabling tasks like filtering, noise reduction, and signal compression.
-
Financial Modeling: Matrices are used in financial modeling to represent portfolios, analyze risks, and optimize investment strategies.
Conclusion: From Simplicity to Complexity and Beyond
While seemingly simple in their representation, 1x1, 2x2, and 4x4 matrices form the foundation of many advanced mathematical concepts and computational techniques. Their dimensions determine their capabilities and applications, influencing the complexity of algorithms and the computational resources required. Their pervasive use across various fields highlights their importance as fundamental building blocks for solving complex problems in diverse domains. Understanding their properties and limitations is crucial for anyone working in fields involving linear algebra, computer science, engineering, and data science. The journey from the trivial 1x1 to the powerful 4x4 matrix underscores the beauty and utility of matrix algebra in the modern world.
Latest Posts
Latest Posts
-
How To Calculate Percentage From Marks
May 14, 2025
-
Words Starting With Q U E
May 14, 2025
-
Why Left Ventricle Is Thicker Than Right Ventricle
May 14, 2025
-
How Many Sides Does A Polygon Have
May 14, 2025
-
How Many Kilos Is 200 Pounds
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 2 X 2 4 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.