1 Out Of 12 As A Percentage
Juapaving
May 10, 2025 · 5 min read
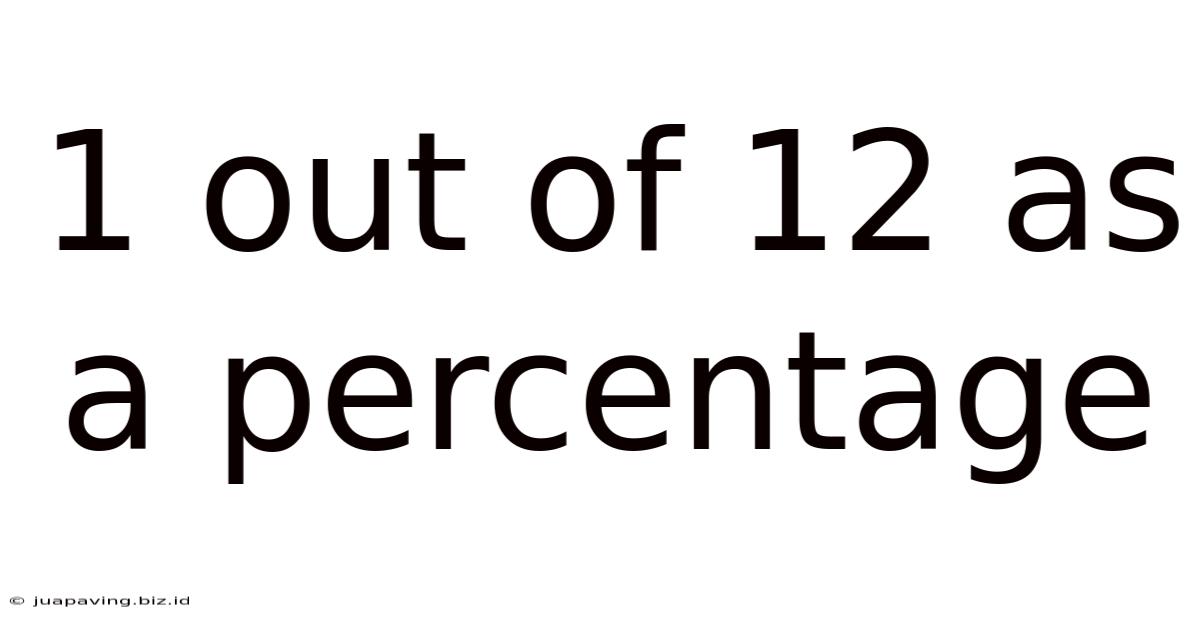
Table of Contents
1 out of 12 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide dives deep into the seemingly simple calculation of "1 out of 12 as a percentage," exploring the underlying concepts, demonstrating the calculation process, and illustrating its practical applications. We'll also look at how to express this fraction in different ways and tackle related percentage problems.
Understanding Fractions and Percentages
Before we delve into the specific calculation, let's solidify our understanding of the building blocks: fractions and percentages.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts that make up the whole. In our case, "1 out of 12" is represented as the fraction 1/12.
Percentages: Expressing Parts per Hundred
A percentage is a way of expressing a fraction or a proportion as a number out of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Percentages are denoted by the symbol "%". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 1 out of 12 as a Percentage
To convert the fraction 1/12 into a percentage, we need to express it as a fraction with a denominator of 100. There are two primary methods to achieve this:
Method 1: Direct Conversion using Division
This method involves dividing the numerator by the denominator and then multiplying the result by 100.
- Divide the numerator by the denominator: 1 ÷ 12 = 0.083333...
- Multiply the result by 100: 0.083333... × 100 = 8.3333...%
Therefore, 1 out of 12 is approximately 8.33%. The recurring decimal indicates that the percentage is an approximation. For most practical purposes, rounding to two decimal places (8.33%) is sufficient.
Method 2: Finding an Equivalent Fraction
This method involves finding an equivalent fraction with a denominator of 100. While this isn't always straightforward, it can be helpful for understanding the underlying concept. Unfortunately, there's no easy way to directly convert 1/12 to a fraction with a denominator of 100. The direct division method is generally preferred for this specific calculation.
Rounding and Precision
The result of converting 1/12 to a percentage is a recurring decimal (8.333...). The level of precision required depends on the context. For general purposes, rounding to two decimal places (8.33%) is usually sufficient. However, for scientific or financial applications, you might need more decimal places or use a fractional representation.
Practical Applications of 1 out of 12 as a Percentage
The ability to calculate percentages like 1 out of 12 has numerous practical applications:
1. Statistics and Probability
Imagine you're analyzing survey data. If 1 out of 12 respondents chose a particular option, you can express this as 8.33%. This allows for easy comparison and visualization of the results.
2. Finance and Budgeting
Suppose you're allocating a budget. If you allocate one twelfth of your monthly income to savings, you're saving approximately 8.33% of your monthly income.
3. Performance Measurement
In business, you might be tracking the success rate of a sales campaign. If 1 out of 12 sales leads convert into a sale, the conversion rate is approximately 8.33%.
4. Discounts and Sales
Imagine a store offering a discount on a select number of items. If only 1 out of 12 items are on sale, the percentage of items on sale is approximately 8.33%.
5. Understanding Data in Everyday Life
The ability to understand and calculate percentages, like converting 1 out of 12 into a percentage, allows you to interpret data presented in various contexts—from sports statistics to weather reports, making you a more informed and critical consumer of information.
Related Percentage Problems and Calculations
Let's extend our understanding by exploring some related percentage problems:
Calculating a Percentage of a Whole Number
If you know a percentage and a whole number, you can calculate the part represented by that percentage. For example, what is 8.33% of 144?
- Convert the percentage to a decimal: 8.33% = 0.0833
- Multiply the decimal by the whole number: 0.0833 × 144 ≈ 12
Therefore, 8.33% of 144 is approximately 12. This shows the inverse relationship between the fraction 1/12 and the percentage 8.33%.
Finding the Percentage One Number Represents of Another
What percentage is 12 of 144?
- Divide the part by the whole: 12 ÷ 144 = 0.0833
- Multiply the result by 100 to express it as a percentage: 0.0833 × 100 = 8.33%
Therefore, 12 represents 8.33% of 144.
Working with More Complex Fractions
Similar principles apply when dealing with more complex fractions. For instance, if you want to calculate "2 out of 12 as a percentage," you would divide 2 by 12 (0.1666...) and then multiply by 100 (approximately 16.67%).
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, including simple conversions like "1 out of 12 as a percentage," is a crucial skill for navigating various aspects of life. Mastering these calculations empowers you to analyze data, make informed decisions, and solve real-world problems with greater confidence and accuracy. Remember to always consider the level of precision required and round appropriately for the given context. By practicing these methods and exploring related percentage calculations, you’ll strengthen your numerical literacy and enhance your ability to interpret and utilize data effectively.
Latest Posts
Latest Posts
-
Relationship Between Momentum And Kinetic Energy
May 11, 2025
-
What Is 10 Of 50 000
May 11, 2025
-
Use Of Matrix In Daily Life
May 11, 2025
-
What Is The Purpose Of A Free Body Diagram
May 11, 2025
-
Density Of Mercury In Kg M3
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1 Out Of 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.